
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ).
).
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() (
(![]() ,
,![]() 是自然对数的底数)上有两个零点,求
是自然对数的底数)上有两个零点,求![]() 的最小值.
的最小值.
【答案】见解析
【解析】(1)函数![]() 的定义域为R,由
的定义域为R,由![]() ,得
,得![]() . ...............2分
. ...............2分
①当![]()
![]()
![]() ,当
,当![]()
![]() ,
,![]() 的变化如下表:
的变化如下表:
|
| 0 |
|
| + | 0 | _ |
| 增 | 极大值 | 减 |
此时,![]() 的递增区间为
的递增区间为![]()
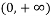
②当![]()
![]() .由
.由![]() ,得
,得![]()
![]()
![]()
![]() ,
,![]() 的变化如下表:
的变化如下表:
|
| 0 |
|
|
|
| + | 0 | - | 0 | + |
| 增 | 极大值 | 减 | 极小值 | 增 |
此时,![]() 的递增区间为
的递增区间为![]()
![]()
![]()
③当![]()
![]() .此时,
.此时,![]() 的递增区间为
的递增区间为![]()
④当![]()
![]() .由
.由![]() ,得
,得![]()
![]()
![]()
![]() ,
,![]() 的变化如下表:.
的变化如下表:.
|
|
|
| 0 |
|
| + | 0 | - | 0 | + |
| 增 | 极大值 | 减 | 极小值 | 增 |
此时,![]() 的递增区间为
的递增区间为![]()
![]()
![]()
综上所述,当![]()
![]() 的递增区间为
的递增区间为![]()
![]()
当![]()
![]() 的递增区间为
的递增区间为![]()
![]()
![]()
当![]()
![]() 的递增区间为
的递增区间为![]()
当![]()
![]() 的递增区间为
的递增区间为![]()
![]()
![]()
(2)当![]() 时,
时,![]() .由(1)可知,
.由(1)可知,![]() 在
在![]()
且![]() 的极大值为
的极大值为![]() ,所以
,所以![]() 在
在![]()
![]()
由![]() ,且
,且![]() 在
在![]()
![]() . ................9分
. ................9分
要想函数![]() 在
在![]() 上还有一个零点,同时考虑到函数
上还有一个零点,同时考虑到函数![]() 在
在![]()
则只需![]() ,且
,且![]() .又因为
.又因为![]()
且![]()
![]() ,
,
所以当![]()
![]() 在
在![]() 还有一个零点,则
还有一个零点,则![]()
综上所述,若![]() 在
在![]() 上有两个零点时,
上有两个零点时,![]()


科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且点P为AD的中点,点Q为SB的中点.

(1)求证:CD⊥平面SAD.
(2)求证:PQ∥平面SCD.
(3)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且A,B,C成等差数列
(1)若b=2 ![]() ,c=2,求△ABC的面积;
,c=2,求△ABC的面积;
(2)若a,b,c成等比数列,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,一个动圆截直线![]() 和
和![]() 所得的弦长分别为8,4.
所得的弦长分别为8,4.
(1)求动圆圆心的轨迹方程![]() ;
;
(2)在轨迹![]() 上是否存在这样的点:它到点
上是否存在这样的点:它到点![]() 的距离等于到点
的距离等于到点![]() 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com