
| A. | $(0,\frac{π}{4})$ | B. | $(0,\frac{π}{6})$ | C. | $(\frac{π}{6},\frac{π}{2})$ | D. | $(\frac{π}{4},\frac{π}{2})$ |
分析 先根据椭圆焦点在y轴上得出$\frac{1}{sinα}$<$\frac{1}{cosα}$,然后由cosα=sin($\frac{π}{2}$-α),进而根据正弦函数的单调性求出α的取值范围.
解答 解:$α∈(0,\frac{π}{2})$,方程x2sinα+y2cosα=1即为
$\frac{{x}^{2}}{\frac{1}{sinα}}$+$\frac{{y}^{2}}{\frac{1}{cosα}}$=1,
∵焦点在y轴上,
∴$\frac{1}{sinα}$<$\frac{1}{cosα}$,
∴sinα>cosα,
即sinα>sin($\frac{π}{2}$-α),
∵0<α<$\frac{π}{2}$,
∴α>$\frac{π}{2}$-α,即$\frac{π}{4}$<α<$\frac{π}{2}$.
故选:D.
点评 本题主要考查了椭圆的标准方程和焦点位置,同时考查诱导公式及三角函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
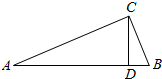
| A. | $\frac{60}{13}$ | B. | $\frac{120}{13}$ | C. | $\frac{50}{13}$ | D. | $\frac{70}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 19 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com