
【题目】设函数![]() .
.
(1)求函数![]() 的极小值;
的极小值;
(2)证明:当![]() 时,不等式
时,不等式![]() 恒成立.
恒成立.
【答案】(1)0;(2)见解析.
【解析】
(1)对函数![]() 求导,分析函数
求导,分析函数![]() 的单调性,即可求出极小值;
的单调性,即可求出极小值;
(2)方法一:不等式![]() 恒成立等价于
恒成立等价于![]() 恒成立. 令
恒成立. 令![]() ,对函数
,对函数![]() 求导,分析函数
求导,分析函数![]() 的单调性,即可证明. 方法二:令
的单调性,即可证明. 方法二:令![]() .通过对函数
.通过对函数![]() 二次求导,分析函数
二次求导,分析函数![]() 的单调性,即可证明.
的单调性,即可证明.
(1)![]() ,
,
则![]() ,令
,令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 为单调递减函数;当
为单调递减函数;当![]() 时,
时,![]() ,
,
![]() 为单调增函数;所以当
为单调增函数;所以当![]() 时,函数
时,函数![]() 取得极小值
取得极小值![]() .
.
(2)方法一:
当![]() 时,不等式
时,不等式![]() 恒成立
恒成立
等价于![]() 恒成立.
恒成立.
令![]() ,
,
则![]() .
.
所以,当![]() 时,
时,![]() ,
,
所以,![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,
,
所以![]() .
.
即当![]() 时,
时,![]() 恒成立.
恒成立.
方法二:当![]() 时,不等式
时,不等式![]() 恒成立
恒成立
等价于![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
令![]() ,
,
则![]() .
.
令![]() ,
,
则![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
故![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
即![]() .
.
所以,当![]() 时,不等式
时,不等式![]() 成立.
成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某手机厂商在销售200万台某型号手机时开展“手机碎屏险”活动、活动规则如下:用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这
元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这![]() 万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取
万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取![]() 名,每名用户赠送
名,每名用户赠送![]() 元的红包,为了合理确定保费
元的红包,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例);
元时愿意购买该“手机碎屏险”的用户比例);
(1)根据上面的数据求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)通过大数据分析,在使用该型号手机的用户中,购机后一年内发生碎屏的比例为![]() .已知更换一次该型号手机屏幕的费用为
.已知更换一次该型号手机屏幕的费用为![]() 元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于
元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于![]() 万元,能否把保费
万元,能否把保费![]() 定为5元?
定为5元?
x | 10 | 20 | 30 | 40 | 50 |
y | 0.79 | 0.59 | 0.38 | 0.23 | 0.01 |
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为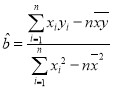 ,
,
![]() ,
,
参考数据:表中![]() 的5个值从左到右分别记为
的5个值从左到右分别记为![]() ,相应的
,相应的![]() 值分别记为
值分别记为![]() ,经计算有
,经计算有![]() ,其中
,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|sinx||cosx|,则下列说法正确的是( )
A.f(x)的图象关于直线![]() 对称
对称
B.f(x)的周期为![]()
C.(π,0)是f(x)的一个对称中心
D.f(x)在区间![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:
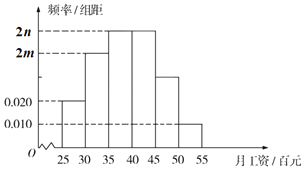
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: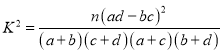 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com