
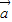 |=4,|
|=4,|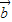 |=3,(2
|=3,(2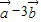 )
)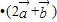 =61,
=61,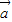 与
与 的夹角θ;
的夹角θ;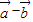 |
| |=4,|
|=4,|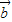 |=3,(2
|=3,(2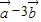 )
)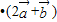 =61,我们可以求出
=61,我们可以求出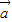 •
•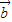 的值,进而根据数量积的夹角公式,求出cos<
的值,进而根据数量积的夹角公式,求出cos<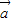 ,
,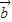 >,进而得到向量
>,进而得到向量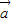 与
与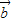 的夹角θ;
的夹角θ;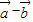 |,我们可以根据(1)中结论,先求出|
|,我们可以根据(1)中结论,先求出|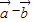 |2的值,然后开方求出答案.
|2的值,然后开方求出答案.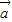 |=4,|
|=4,|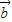 |=3,
|=3,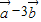 )
)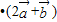 =4|
=4|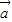 |2-3|
|2-3|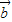 |2-4
|2-4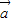 •
•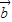 =37-4
=37-4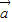 •
•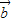 =61
=61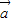 •
•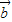 =|
=|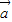 |•|
|•|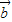 |•cos<
|•cos<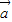 ,
,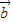 >=-6
>=-6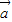 ,
,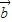 >=-
>=-
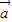 ,
,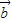 >=120°
>=120°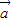 与
与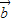 的夹角θ=120°…(8分)
的夹角θ=120°…(8分)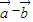 |2=|
|2=|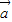 |2+|
|2+|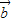 |2-2
|2-2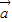 •
•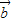 =16+9+12=37
=16+9+12=37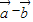 |=
|=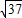 …(14分)
…(14分)

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 2 |
| 4 |
| 5 |
| 12 |
| 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com