
【题目】若函数f(x)=loga|x+1|在区间(﹣2,﹣1)上恒有f(x)>0,则关于a的不等式f(4a﹣1)>f(1)的解集为 .
【答案】(0, ![]() )
)
【解析】解:因为函数f(x))=loga|x+1|在区间(﹣2,﹣1)上恒有f(x)>0,所以0<a<1,且该函数在区间(﹣∞,﹣1)上为增函数,在(﹣1,+∞)上为减函数,
又f(4a﹣1)>f(1),且4a﹣1>﹣1,
所以4a﹣1<1,解得0<a< ![]() ,
,
所以关于a的不等式f(4a﹣1)>f(1)的解集为(0, ![]() ),
),
所以答案是:(0, ![]() ).
).
【考点精析】本题主要考查了函数单调性的判断方法和函数单调性的性质的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设S表示所有大于﹣1的实数构成的集合,确定所有的函数:S→S,满足以下两个条件:
对于S内的所有x和y,f(x+f(y)+xf(y))=y+f(x)+yf(x);在区间﹣1<x<0与x>0的每一个内, ![]() 是严格递增的.求满足上述条件的函数的方程.
是严格递增的.求满足上述条件的函数的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,a1=2,a3=18.数列{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求数列{an},{bn}的通项公式;
(2)设Pn=b1+b4+b7+…+b3n﹣2 , Qn=b10+b12+b14+…+b2n+8 , 其中n=1,2,3,….试比较Pn与Qn的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
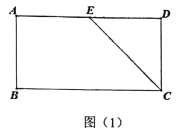
【题目】在矩形![]() 中,
中, ![]() ,
, ![]() 是边
是边![]() 的中点,如图(1),将
的中点,如图(1),将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).
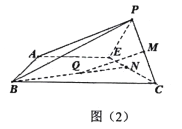
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)是定义在(﹣3,3)上的奇函数,当0<x<3时,函数f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( ) 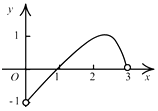
A.(﹣3,﹣ ![]() )∪(0,1)∪(
)∪(0,1)∪( ![]() ,3)
,3)
B.(﹣ ![]() ,﹣1)∪(0,1)∪(
,﹣1)∪(0,1)∪( ![]() ,3)
,3)
C.(﹣3,﹣1)∪(0,1)∪(1,3)
D.(﹣3,﹣ ![]() )∪(0,1)∪(1,3)
)∪(0,1)∪(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C是△ABC的三个内角.
(1)3cos(B﹣C)﹣1=6cosBcosC,求cosA的值;
(2)若sin(A+ ![]() )=2cosA,求A.
)=2cosA,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是抛物线y2=8x上的一个动点,Q是圆(x﹣3)2+(y﹣1)2=1上的一个动点,N(2,0)是一个定点,则|PQ|+|PN|的最小值为( )
A.3
B.4
C.5
D.![]() +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com