
分析 (1)利用等差数列的通项公式及其求和公式即可得出.
(2)利用等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,
∵a1=2,S3=9.∴3×2+$\frac{3×2}{2}$d=9,解得d=1.
∴an=a1+(n-1)d=n+1.
(2)由(1)知${2^{a_n}}={2^{n+1}}$,
∴$\left\{{{2^{a_n}}}\right\}$是以4为首项,2为公比的等比数列,
∴${S_n}=\frac{{4(1-{2^n})}}{1-2}=4•{2^n}-4={2^{n+2}}-4$.
点评 本题考查了等差数列与等比数列的通项公式及其求和公式,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,0) | C. | [1,3) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某班n名学生的综合素质测评成绩(百分制)频率分布直方图如图所示,已知70~80分数段的学生人数为27人,90~95分数段的学生中女生为2人.
某班n名学生的综合素质测评成绩(百分制)频率分布直方图如图所示,已知70~80分数段的学生人数为27人,90~95分数段的学生中女生为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
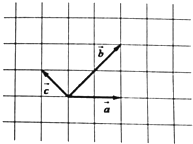 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3≤a≤6 | B. | a≥6或a≤-3 | C. | -3<a<6 | D. | a>6或a<-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com