
【题目】如图四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,且CD=2,AB=BC=PA=1,PD= ![]() .
. 
(1)求三棱锥A﹣PCD的体积;
(2)问:棱PB上是否存在点E,使得PD∥平面ACE?若存在,求出 ![]() 的值,并加以证明;若不存在,请说明理由.
的值,并加以证明;若不存在,请说明理由.
【答案】
(1)解:取CD中点G,连接AG,
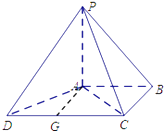
∵CD=2AB,AB∥CD,
∴AB∥GC,AB=GC,
∴四边形AGCB为平行四边形,
∴∠AGD=∠DCB=∠ABC=90°,
在Rt△AGD中,∵AG=BC=1,DG= ![]() CD=1,
CD=1,
∴AD= ![]() =
= ![]() ,
,
∴PD2=3=PA2+AD2,
∴∠PAD=90°,即PA⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PA⊥平面ABCD,
∵S△ACD= ![]() =1,
=1,
∴VA﹣PCD=VP﹣ACD= ![]()
= ![]() =
= ![]() .
.
(2)解:棱PB上存在点E,当 ![]() =
= ![]() 时,PD∥平面ACE.
时,PD∥平面ACE.
证明:连接BD交AC于点O,连接OE.
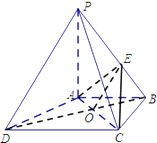
∵AB∥CD,CD=2AB,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,又
,又 ![]() ,
,
∴ ![]() ,
,
∴OE∥DP,
又OE平面ACE,PDACE,
∴PD∥ACE.
【解析】(1)取CD中点G,连接AG,利用已知可得:四边形AGCB为平行四边形,∠AGD=∠DCB=∠ABC=90°,在Rt△AGD中,AG=BC=1,DG= ![]() CD=1,利用勾股定理与逆定理可得:PA⊥AD.利用面面垂直的性质定理可得:PA⊥平面ABCD,利用VA﹣PCD=VP﹣ACD=
CD=1,利用勾股定理与逆定理可得:PA⊥AD.利用面面垂直的性质定理可得:PA⊥平面ABCD,利用VA﹣PCD=VP﹣ACD= ![]() ,即可得出.(2)棱PB上存在点E,当
,即可得出.(2)棱PB上存在点E,当 ![]() =
= ![]() 时,PD∥平面ACE.连接BD交AC于点O,连接OE.利用平行线分线段成比例定理再三角形中的应用:可得OE∥DP.
时,PD∥平面ACE.连接BD交AC于点O,连接OE.利用平行线分线段成比例定理再三角形中的应用:可得OE∥DP.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】不等式(x+ ![]() )(
)( ![]() ﹣x)≥0的解集是( )
﹣x)≥0的解集是( )
A.{x|﹣ ![]() ≤x≤
≤x≤ ![]() }
}
B.{x|x≤﹣ ![]() 或x≥
或x≥ ![]() }??
}??
C.{x|x<﹣ ![]() 或x>
或x> ![]() }
}
D.{x|﹣ ![]() <x<
<x< ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(18)(本小题满分12分)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙中心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名B1,B2,
B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。
(I)求接受甲种心理暗示的志愿者中包含A1但不包含B3的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和Sn=2n+r.
(1)求实数r的值和{an}的通项公式;
(2)若数列{bn}满足b1=1,bn+1﹣bn=log2an+1 , 求bn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,
中, ![]() 与
与![]() 均为边长为2的正方形,
均为边长为2的正方形, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用简单随机抽样方法从含有6个个体的总体中,抽取一个容量为2的样本,某一个体a“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到”的概率分别是
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=0,nan+1=Sn+n(n+1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足an+log3n=log3bn , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,侧棱PA与底面成45°的角,M,N,分别是AB,PC的中点; 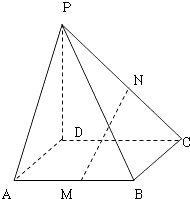
(1)求证:MN∥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com