
 ,求出现1点或2点的概率;
,求出现1点或2点的概率; ,P(B)=
,P(B)= ,求这3只球中既有红球又有白球的概率。
,求这3只球中既有红球又有白球的概率。科目:高中数学 来源: 题型:
A.360种 B.840种 C.600种 D.1 680种
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:解答题
(本小题满分13分)
已知m,n表示先后抛掷一个骰子所得到正面向上的点数,方程C: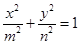
(1)求共可以组成多少个不同的方程C;
(2)求能组成落在区域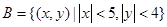 且焦点在X轴的椭圆的概率;
且焦点在X轴的椭圆的概率;
(3)在已知方程C为落在区域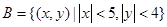 且焦点在X轴的椭圆的情况下,求离心率为
且焦点在X轴的椭圆的情况下,求离心率为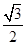 的概率
的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com