解:(Ⅰ)∵点P
n(n,S
n)都在函数f(x)=x
2+2x的图象上,
∴
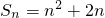
.
当n=1时,a
1=S
1=3;
当n≥2时,
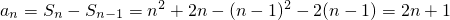
,
当n=1时,也满足.
故a
n=2n+1.
(Ⅱ)由f(x)=x
2+2x求导可得,f′(x)=2x+2
∵过点P
n(n,S
n)的切线的斜率为k
n,∴k
n=2n+2.
又∵
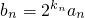
,
∴
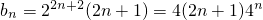
.
∴
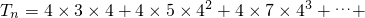
4(2n+1)•4
n…①
由①×4可得:

4(2n+1)•4
n+1…②
①-②可得:
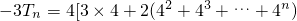
-(2n+1)•4
n+1]
=
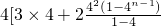
-(2n+1)•4
n+1].
∴
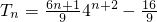
.
(Ⅲ)∵Q={x|x=2n+2,n∈N
*},R={x|x=4n+2,n∈N
*}
∴Q∩R=R,又∵c
n∈Q∩R,其中c
1是Q∩R中的最小数,
∴c
1=6,∴c
10=4m+6,m∈N
*,({c
n}的公差是4 的倍数!)
又∵110<c
10<115
∴

解得m=27.
分析:(Ⅰ)根据点在函数图象上,则点满足函数解析式,得到S
n的表达式,进而求得数列{a
n}的通项公式;
(Ⅱ)根据题中条件求出kn的表达式,结合(1)求得的数列{a
n}的通项公式,即可求得数列{b
n}的通项公式,进而可以利用错位相消法求出数列{b
n}的前n项和T
n.
(Ⅲ)由“Q={x|x=2n+2,n∈N
*},R={x|x=4n+2,n∈N
*}”求得交集,再由“c
n∈Q∩R,其中c
1是Q∩R中的最小数”可求得c
1=6.最后由{c
n}是公差是4的倍数求得c
10=4m+6,则110<c
10<115求解即可.
点评:本题集函数、导数、数列、不等式于一体,体现了知识间的交汇与融合,同时又考查了数列的基本解题方法,考查了学生分析问题和解决问题.强调在“知识的交汇处”命制试题,是近年高考命题的趋势.

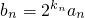 ,求数列{bn}的前n项和为Tn;
,求数列{bn}的前n项和为Tn;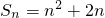 .
.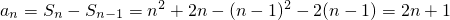 ,
,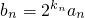 ,
,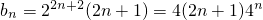 .
.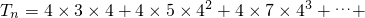 4(2n+1)•4n…①
4(2n+1)•4n…① 4(2n+1)•4n+1…②
4(2n+1)•4n+1…②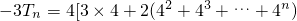 -(2n+1)•4n+1]
-(2n+1)•4n+1]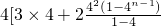 -(2n+1)•4n+1].
-(2n+1)•4n+1].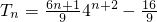 .
. 解得m=27.
解得m=27.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<