设等差数列的首项及公差均为非负整数,项数不少于3,且各项之和为972,这样的数列共有________个.
4
分析:设等差数列首项为a,公差为d,由条件可得[2a+(n-1)d]n=2×97
2,因为n为不小于3的自然数,97为素数,故n的值只可能为97,2×97,97
2,2×97
2四者之一.分d>0、
d=0两种情况,分别求出n、a、d,从而得出结论.
解答:设等差数列首项为a,公差为d,依题意有
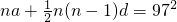
,即[2a+(n-1)d]n=2×97
2 .
因为n为不小于3的自然数,97为素数,故n的值只可能为97,2×97,97
2,2×97
2四者之一.
若d>0,则知2×97
2≥n(n-1)d≥n(n-1)>(n-1)
2.
故只可能有n=97.于是 a+48d=97.
此时可得n=97,d=1,a=49 或 n=97,d=2,a=1.
若d=0时,则由(3)得na=97
2,此时n=97,a=97 或 n=97
2,a=1.
故符合条件的数列共有4个.
故答案为 4.
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式,等差数列的前n项和公式的应用,属于中档题.

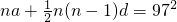 ,即[2a+(n-1)d]n=2×972 .
,即[2a+(n-1)d]n=2×972 . 
