
【题目】如图,已知图形ABCDEF,内部连有线段.
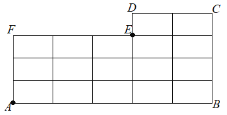
(1)由点A沿着图中的线段到达点E的最近路线有多少条?
(2)由点A沿着图中的线段到达点C的最近路线有多少条?
(3)求出图中总计有多少个矩形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意转化条件为点A需向右移动3次、向上移动3次,结合组合的知识即可得解;
(2)设出直线![]() 上其它格点为
上其它格点为![]() 、
、![]() 、
、![]() ,按照
,按照![]() 、
、![]() 、
、![]() 、
、![]() 分类,结合分步乘法、组合的知识即可得解;
分类,结合分步乘法、组合的知识即可得解;
(3)由题意转化条件为从竖线中选出两条、横线中选出两条组成图形,按照矩形的边在不在![]() 上分类,利用分步乘法、组合的知识即可得解.
上分类,利用分步乘法、组合的知识即可得解.
(1)由题意点A沿着图中的线段到达点E的最近路线需要移动6次:向右移动3次,向上移动3次,故点A到达点E的最近路线的条数为![]() ;
;
(2)设点![]() 、
、![]() 、
、![]() 的位置如图所示:
的位置如图所示:
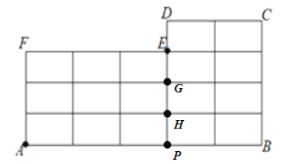
则点A沿着图中的线段到达点C的最近路线可分为4种情况:
①沿着![]() ,共有
,共有![]() 条最近路线;
条最近路线;
②沿着![]() ,共有
,共有![]() 条最近路线;
条最近路线;
③沿着![]() ,共有
,共有![]() 条最近路线;
条最近路线;
④沿着![]() ,共有
,共有![]() 条最近路线;
条最近路线;
故由点A沿着图中的线段到达点C的最近路线有![]() 条;
条;
(3)由题意,要组成矩形则应从竖线中选出两条、横线中选出两条,可分为两种情况:
①矩形的边不在![]() 上,共有
上,共有![]() 个矩形;
个矩形;
②矩形的一条边在![]() 上,共有
上,共有![]() 个矩形;
个矩形;
故图中共有![]() 个矩形.
个矩形.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,实轴长为6,渐近线方程为
,实轴长为6,渐近线方程为![]() ,动点
,动点![]() 在双曲线左支上,点
在双曲线左支上,点![]() 为圆
为圆![]() 上一点,则
上一点,则![]() 的最小值为
的最小值为
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如上图.现在图(3)中随机选取一个点,则此点取自阴影部分的概率为________

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下边的折线图给出的是甲、乙两只股票在某年中每月的收盘价格,已知股票甲的极差是6.88元,标准差为2.04元;股票乙的极差为27.47元,标准差为9.63元,根据这两只股票在这一年中的波动程度,给出下列结论:①股票甲在这一年中波动相对较小,表现的更加稳定;②购买股票乙风险高但可能获得高回报;③股票甲的走势相对平稳,股票乙的股价波动较大;④两只般票在全年都处于上升趋势.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 离心率为
离心率为![]() ,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线
,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线![]() :
:![]() 相切.
相切.
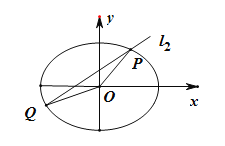
(1)求椭圆C的方程;
(2)设不过原点O的直线![]() 与该椭圆交于P、Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
与该椭圆交于P、Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程,并求其离心率;
的方程,并求其离心率;
(2)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),点
上),点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与
与![]() 交于另一点
交于另一点![]() .设
.设![]() 为原点,判断直线
为原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时10分钟.那么经过5分钟后,沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度之比是(假定沙堆的底面是水平的)( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,
中,![]() 菱形
菱形![]() 所在的平面,
所在的平面,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 上的点.
上的点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,当
的中点,当![]() 时,是否存在点
时,是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 的所成角的正弦值为
的所成角的正弦值为![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com