
【题目】已知函数f(x)=1﹣ ![]() 在R上是奇函数.
在R上是奇函数.
(1)求a;
(2)对x∈(0,1],不等式sf(x)≥2x﹣1恒成立,求实数s的取值范围;
(3)令g(x)= ![]() ,若关于x的方程g(2x)﹣mg(x+1)=0有唯一实数解,求实数m的取值范围.
,若关于x的方程g(2x)﹣mg(x+1)=0有唯一实数解,求实数m的取值范围.
【答案】
(1)解:由题意知f(0)=0.即 ![]() ,
,
所以a=2.此时f(x)= ![]() ,
,
而f(﹣x)= ![]() ,
,
所以f(x)为奇函数,故a=2为所求
(2)解:由(1)知 ![]() ,
,
因为x∈(0,1],所以2x﹣1>0,2x+1>0,
故sf(x)≥2x﹣1恒成立等价于s≥2x+1恒成立,
因为2x+1∈(2,3],所以只需s≥3即可使原不等式恒成立.
故s的取值范围是[3,+∞)
(3)解:因为 ![]() .
.
所以g(2x)﹣mg(x+1)= ![]() .
.
整理得22x﹣2m2x﹣m+1=0.
令t=2x>0,则问题化为t2﹣2mt﹣m+1=0有一个正根或两个相等正根.
令h(t)=t2﹣2mt﹣m+1(t>0),则函数h(t)=t2﹣2mt﹣m+1在(0,+∞)上有唯一零点.
所以h(0)≤0或 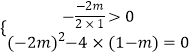 ,
,
由h(0)≤0得m≥1,
易知m=1时,h(t)=t2﹣2t符合题意;
由 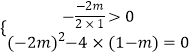 解得
解得  ,
,
所以m= ![]() .
.
综上m的取值范围是 ![]()
【解析】(1)根据f(0)=0可求得a的值,然后验证a的取值满足函数为奇函数;(2)分离参数法,将问题转化为函数的最值问题求解;(3)可先将方程化简,然后问题转化为一元二次方程在指定区间上根的分布问题,然后再进一步求解.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sin(2x+ ![]() )的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的
)的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的 ![]() 倍,所得图象关于直线x=
倍,所得图象关于直线x= ![]() 对称,则φ的最小正值为 .
对称,则φ的最小正值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆过点A(0,﹣6)和B(1,﹣5),且圆心在直线l:x﹣y+1=0上.
(1)求圆心为C的圆的标准方程;
(2)过点M(2,8)作圆的切线,求切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各6名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,则甲班样本数据的众数和乙班样本数据的中位数分别是( ) 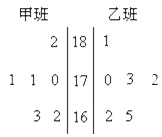
A.170,170
B.171,171
C.171,170
D.170,172
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对于任意x∈R有 ![]() ,且当x∈[﹣1,1]时,f(x)=x2+1,则以下命题正确的是: ①函数数y=f(x)是周期为2的偶函数;
,且当x∈[﹣1,1]时,f(x)=x2+1,则以下命题正确的是: ①函数数y=f(x)是周期为2的偶函数;
②函数y=f(x)在[2,3]上单调递增;
③函数 ![]() 的最大值是4;
的最大值是4;
④若关于x的方程[f(x)]2﹣f(x)﹣m=0有实根,则实数m的范围是[0,2];
⑤当x1 , x2∈[1,3]时, ![]() .
.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)是定义在(0,+∞)上的函数,并且满足下面三个条件: ①对任意正数x,y,都有f(xy)=f(x)+f(y);
②当x>1时,f(x)>0;
③f(3)=1,
(1)求f(1), ![]() 的值;
的值;
(2)判断函数f(x)在区间(0,+∞)上单调性,并用定义给出证明;
(3)对于定义域内的任意实数x,f(kx)+f(4﹣x)<2(k为常数,且k>0)恒成立,求正实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1 , 底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别是A1B1、A1A的中点. 
(1)求 ![]() 的长;
的长;
(2)求cos( ![]()
![]() )的值;
)的值;
(3)求证A1B⊥C1M.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com