考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)欲证AB1∥平面BC1D,只需证明AB1平行平面BC1D中的一条直线,利用三角形的中位线平行与第三边,构造一个三角形AB1C,使AB1成为这个三角形中的边,而中位线OD恰好在平面BC1D上,就可得到结论.
(2)建系D-xyz,分别求出平面BC1D和平面BCC1的法向量,代入向量夹角公式,可得答案.
解答:
证明:(1)连接B
1C,设B
1C与BC
1相交于点O,连接OD,
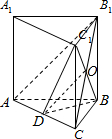
∵四边形BCC
1B是平行四边形,
∴点O为B
1C的中点,
∵D为AC的中点,
∴OD为△AB
1C的中位线,
∴OD∥AB
1,
∵OD?平面BC
1D,AB
1?平面BC
1D,
∴AB
1∥平面BC
1D …(5分)
解:(2)建系D-xyz如图.
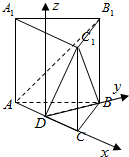
由题意可知:D(0,0,0),C(1,0,0),B(0,
,0),C
1(1,0,
),则
=(1,0,
),
=(0,
,0),
=(0,0,
),
=(-1,
,0),
设平面BC
1D和平面BCC
1的法向量分别为:
=(x,y,z),
=(a,b,c),
则
,即
,令x=
,则:
=(
,0,-1),
,即
,令a=
,则:
=(
,1,0),
故二面角D-BC
1-C的平面角θ的余弦值cosθ=
=
点评:本题考察了线面平行判定定理的应用和二面角的作法和求法,解决二面角问题关键是要转化为向量夹角问题.

 已知三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为
已知三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为


