【题目】若四面体的六条棱长分别为2,3,4,5, 6,7,则不同的形状有______种(若两个四面体经适当放置后可完全重合,则认为是相同的形状).
【答案】10.
【解析】
将长为k的棱记为
.考虑
.
(1) 共面,则该面的另一边必为
.
(i)若
按顺时针方向组成三角形(均指从形内向该面看三边的绕向,下同),则边
不能取
(否则,将使
的三边为2,5,7,矛盾)
若取
,
,有2种情况;
若取
,
,也有2种情况. 共得4种情况.
(ii)若按逆时针方向组成三角形,类似也得4种情况.
(2)异面,设
,
.则其余四条边，每一条皆与相邻，于是
所在面的另一条边必为.
(i)若
按顺时 针方向组成三角形,不妨设
,
,剩 下两条边,
不能取,故只有
,
,得1 种情况.(ii)若按逆时针方向组成三角形,类似也得1种情况. 因此,本题中不同的形状有10种.
故答案为：10
科目：高中数学 来源： 题型：
【题目】设有限数列
，定义集合
为数列
的伴随集合．
（Ⅰ）已知有限数列
和数列
．分别写出
和
的伴随集合；
（Ⅱ）已知有限等比数列
，求的伴随集合
中各元素之和
；
（Ⅲ）已知有限等差数列
，判断
是否能同时属于的伴随集合，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据统计，某蔬菜基地西红柿亩产量的增加量
（百千克）与某种液体肥料每亩使用量
（千克）之间的对应数据的散点图，如图所示.
（1）依据数据的散点图可以看出，可用线性回归模型拟合与的关系，请计算相关系数
并加以说明（若
，则线性相关程度很高，可用线性回归模型拟合）；
（2）求关于的回归方程，并预测液体肥料每亩使用量为
千克时，西红柿亩产量的增加量约为多少？
附：相关系数公式
，回归方程
中斜率和截距的最小二乘估计公式分别为：
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形
为一张台球桌面，
，
.从点
击出一个球，其可无限次经台球桌四边反弹运行.已知该球经过矩形的中心
.
（1）试求所有整点
的个数，使得该球可以经过点
；
（2）若该球在上述
、两点间的最短路径长为
，求的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】每年3月21日是世界睡眠日，良好的睡眠状况是保持身体健康的重要基础.为了做好今年的世界睡眠日宣传工作，某社区从本辖区内同一年龄层次的人员中抽取了100人，通过问询的方式得到他们在一周内的睡眠时间(单位：小时)，并绘制出如右的频率分布直方图：
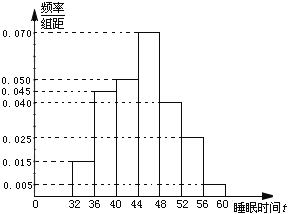
(Ⅰ)求这100人睡眠时间的平均数
(同一组数据用该组区间的中点值代替，结果精确到个位)；
(Ⅱ)由直方图可以认为，人的睡眠时间
近似服从正态分布
，其中
近似地等于样本平均数，
近似地等于样本方差
，
.假设该辖区内这一年龄层次共有10000人，试估计该人群中一周睡眠时间位于区间(39.2，50.8)的人数.
附：
.若随机变量
服从正态分布，则
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设椭圆
(
)的左、右焦点分别为
，过
的直线交椭圆于
，
两点，若椭圆
的离心率为
，
的周长为
.
(1)求椭圆的方程；
(2)设不经过椭圆的中心而平行于弦
的直线交椭圆于点
，
，设弦，
的中点分别为
，证明：
三点共线.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的
倍，P为侧棱SD上的点.
（Ⅰ）求证：AC⊥SD；
（Ⅱ）若SD⊥平面PAC，求二面角P-AC-D的大小；
（Ⅲ）在（Ⅱ）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC.若存在，求SE：EC的值；若不存在，试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
