
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:
时,证明:![]() 对
对![]() 恒成立.
恒成立.
【答案】(1)答案见解析;(2)证明见解析.
【解析】分析:(1)由函数的解析式可得![]() ,分类讨论有:
,分类讨论有:
①若![]() ,当
,当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减.
单调递减.
②若![]() ,当
,当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增.当
单调递增.当![]() 时,
时,![]() 单调递减.
单调递减.
③若![]() ,当
,当![]() 时,
时,![]() 单调递减.
单调递减.
④若![]() ,当
,当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减.
单调递减.
⑤若![]() ,当
,当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增.
单调递增.
(2)不等式等价于![]() .
.
令![]() ,由均值不等式可得
,由均值不等式可得![]() .结合(1)的结论可知当
.结合(1)的结论可知当![]() 时,
时,![]() .令
.令![]() ,则
,则![]() ,故
,故![]() ,原命题成立.
,原命题成立.
详解:(1)![]() ,
,
①若![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
②若![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增.
单调递增.
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
③若![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
④若![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
⑤若![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增.
单调递增.
(2)将![]() 整理可得:
整理可得:
![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,
当且仅当![]() 时取等号,即
时取等号,即![]() .
.
当![]() 时,由(1)可知,
时,由(1)可知,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() .
.
令![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() ,
,
即![]() 对
对![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
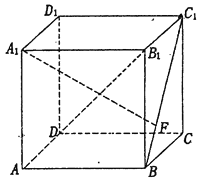
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法错误的是( )
上的动点,则下列说法错误的是( )
A. 无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
B. 无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
C. 当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 与相交于一点,记为点
与相交于一点,记为点![]() ,且
,且![]()
D. 当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0).且点C与点D在函数f(x)= 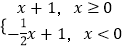 的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( )
的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( ) 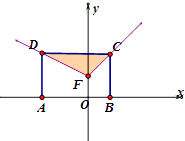
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算,若今年的实际销售单价为![]() 元/件
元/件![]() ,则新增的年销量
,则新增的年销量![]() (万件).
(万件).
(Ⅰ)写出今年商户甲的收益![]() (单位:万元)与
(单位:万元)与![]() 的函数关系式;
的函数关系式;
(Ⅱ)商户甲今年采取降低单价提高销量的营销策略,是否能获得比往年更大的收益(即比往年收益更多)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1,(a>b>0)的离心率为
=1,(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+ ![]() =0)且不垂直于x轴直线l椭圆C相交于A、B两点. (Ⅰ)求椭圆C的方程;
=0)且不垂直于x轴直线l椭圆C相交于A、B两点. (Ⅰ)求椭圆C的方程;
(Ⅱ)求 ![]()
![]() 取值范围;
取值范围;
(Ⅲ)若B关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com