
【题目】(2016·雅安高一检测)已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2),
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a2=2,a5=8.
(1)求{an}的通项公式;
(2)各项均为正数的等比数列{bn}中,b1=1,b2+b3=a4,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
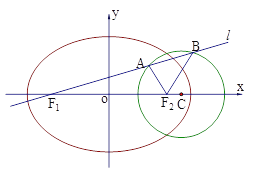
【题目】已知如图,圆![]() 、椭圆
、椭圆![]() 均经过点M
均经过点M![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,椭圆
,椭圆![]() 的两焦点分别为
的两焦点分别为![]() .
.
(Ⅰ)分别求圆![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,试探究
两点,试探究![]() 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径![]()
,此时圆内接正六边形的周长为![]()
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据: ![]()
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在R上的奇函数,对x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(-1)=2.
(1)求证:f(x)为奇函数;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在[-2,4]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=![]() (a∈R).
(a∈R).
(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com