
 +
+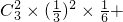
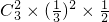 =
=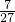 .
.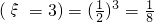 ;
;
 =
=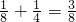 ;
;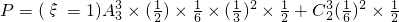 =
= ;
;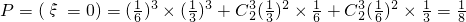 .
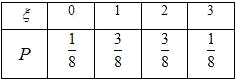
.
 .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:设计必修四数学苏教版 苏教版 题型:044
三人夺球的游戏的规则是:在小球上均匀装上三条绳子,由三人在一水平面上分别拉绳,要求每两人与球连线夹角相等,得到小球者为胜.现有甲、乙、丙三人玩此游戏,若甲、乙两人的力量相同,均为a N,试探究丙需要多少力量小球静止?若甲、乙两人的力量不等,则小球有可能静止吗?
查看答案和解析>>
科目:高中数学 来源:设计必修四数学人教A版 人教A版 题型:044
三人夺球的游戏的规则是:在小球上均匀装上三条绳子,由三人在一水平面上分别拉绳,要求每两人与球连线夹角相等,得到小球者为胜.现有甲、乙、丙三人玩此游戏,若甲、乙两人的力量相同,均为a N,试探究丙需要多少力量小球才静止?若甲、乙两人的力量不等,则小球有可能静止吗?
查看答案和解析>>
科目:高中数学 来源:2010年山东省威海市高考模拟数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com