
【题目】已知函数![]() ,其中
,其中![]() .
.![]() 是自然对数的底数.
是自然对数的底数.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .求实数
.求实数![]() 的值;
的值;
(2)① 若![]() 时,函数
时,函数![]() 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数![]() 的取值范围;
的取值范围;
② 若![]() ,
,![]() .若
.若![]() 对一切正实数
对一切正实数![]() 恒成立,求实数
恒成立,求实数![]() 的最大值(用
的最大值(用![]() 表示).
表示).
【答案】(1)![]() .(2)①
.(2)①![]() ②
②![]()
【解析】
试题(1)由导数几何意义得![]() ,又过过点(1,0),因此可列方程组
,又过过点(1,0),因此可列方程组![]() ,解得
,解得![]() (2)①由题意得,导函数有两个不同的零点,即
(2)①由题意得,导函数有两个不同的零点,即![]() 有两个不同的解,研究目标函数
有两个不同的解,研究目标函数![]()
![]() 得
得![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数,因此
上为增函数,因此![]() ②先化简不等式:
②先化简不等式:![]() ,再分别求证
,再分别求证![]() ,
,![]() (当且仅当都在
(当且仅当都在![]() 处取到等号),最后利用不等式性质得
处取到等号),最后利用不等式性质得![]()
试题解析: (1) 由题意知曲线![]() 过点(1,0),且
过点(1,0),且![]() ;又因为
;又因为![]() ,则有
,则有![]() 解得
解得![]() .
.
(2)①当![]() 时,函数
时,函数![]() 的导函数
的导函数![]() ,若
,若![]() 时,得
时,得![]() ,设
,设![]()
![]() . 由
. 由![]()
![]() ,得
,得![]() ,
,![]() . 当
. 当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上为减函数,
上为减函数,![]() ;当
;当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,![]() ;所以,当且仅当
;所以,当且仅当![]() 时,
时,![]() 有两个不同的解,设为
有两个不同的解,设为![]() ,
,![]()
![]() .
.

此时,函数![]() 既有极大值,又有极小值.
既有极大值,又有极小值.
②由题意![]() 对一切正实数
对一切正实数![]() 恒成立,取
恒成立,取![]() 得
得![]() .下证
.下证![]() 对一切正实数
对一切正实数![]() 恒成立.首先,证明
恒成立.首先,证明![]() . 设函数
. 设函数![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;得
;得![]() ,即
,即![]() ,当且仅当都在
,当且仅当都在![]() 处取到等号. 再证
处取到等号. 再证![]() . 设
. 设![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;得
;得![]() ,即
,即![]() ,当且仅当都在
,当且仅当都在![]() 处取到等号. 由上可得
处取到等号. 由上可得![]() ,所以
,所以![]() ,即实数
,即实数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知![]() ,且2an+1=an+1(n∈N*).
,且2an+1=an+1(n∈N*).
(1)求证:数列{an-1}是等比数列;
(2)若bn=nan,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:

(1)求![]() 的值;
的值;
(2)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
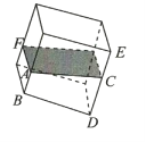
【题目】在一个长方体的容器中,里面装有少量的水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与两个定点O(0,0),A(3,0)的距离的比值为2,点P的轨迹为曲线C.
(1)求曲线C的轨迹方程
(2)过点(﹣1,0)作直线与曲线C交于A,B两点,设点M坐标为(4,0),求△ABM面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为![]() 的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
(1)求抛物线C的标准方程;
(2)设点P为抛物线C上异于A,B的点,直线PA与PB分别交抛物线C的准线于E,G两点,x轴与准线的交点为H,求证:HGHE为定值,并求出定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是______
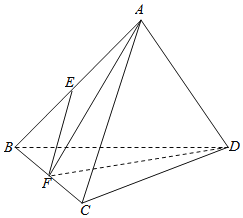
①异面直线AB与CD所成角为90°;
②直线AB与平面BCD所成角为60°;
③直线EF∥平面ACD
④平面AFD⊥平面BCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com