Question

【题目】如图，平面平面，其中为矩形，为梯形，，，.

（Ⅰ）求证：平面；

（Ⅱ）若二面角的平面角的余弦值为，求的长.

Answer 1

【答案】（Ⅰ）见解析； （Ⅱ） .

【解析】

（Ⅰ）由条件易得和，从而可证得平面；

（Ⅱ）设AB＝x．以F为原点，AF，FE所在的直线分别为x轴，y轴建立空间直角坐标系，平面ABF的法向量可取＝(0，1，0)，通过求解平面BFD的法向量，进而利用法向量求二面角的余弦值列方程求解即可.

(Ⅰ)平面平面,且为矩形，

平面，又平面, ，又且

平面.

(Ⅱ)设AB＝x．以F为原点，AF，FE所在的直线分别为x轴，y轴建立空间直角坐标系．

则F(0，0，0)，A(－2，0，0)，E(0，，0)，D(－1，，0)，B(－2，0，x)，

所以＝(1，－，0)，＝(2，0，－x)．

因为EF⊥平面ABF，所以平面ABF的法向量可取＝(0，1，0)．

设＝(x1，y1，z1)为平面BFD的法向量，

则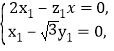所以，可取＝(，1，)．

因为cos<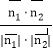，>＝＝，得x＝，所以AB＝．