
【题目】现有下列四个结论,其中所有正确结论的编号是___________.
①若![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,
,![]() ,
,![]() 是等差数列
是等差数列![]() 的前
的前![]() 项,则
项,则![]() ;
;
③“![]() ”的一个必要不充分条件是“
”的一个必要不充分条件是“![]() ”;
”;
④“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”.
”.
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从某养殖场购进某品种河蟹,并随机抽取了 100只进行统计,按重量分类统计,得到频率分布直方图如下:
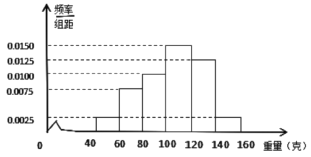
(1)记事件![]() 为“从这批河蟹中任取一只,重量不超过120克”,估计
为“从这批河蟹中任取一只,重量不超过120克”,估计![]() ;
;
(2)试估计这批河蟹的平均重量;
(3)该经销商按有关规定将该品种河蟹分三个等级,并制定出销售单价如下:
等级 | 特级 | 一级 | 二级 |
重量 |
|
|
|
单价(元/只) | 40 | 20 | 10 |
试估算该经销商以每千克至多花多少元(取整)收购这批河蟹,才能获利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() ,与以右焦点
,与以右焦点![]() 为圆心,半径为
为圆心,半径为![]() 的圆
的圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)线段![]() 是椭圆
是椭圆![]() 过右焦点
过右焦点![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面积的最大值以及取最大值时实数
的面积的最大值以及取最大值时实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n为平面α外两条直线,其在平面α内的射影分别是两条直线m1和n1,给出下列4个命题:①m1∥n1m∥n;②m∥nm1与n1平行或重合;③m1⊥n1m⊥n;④m⊥nm1⊥n1.其中所有假命题的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com