
(本题满分16分)本题共有3个小题,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分7分.
已知函数![]() (
(![]() )为偶函数.
)为偶函数.
(1)求常数![]() 的值;
的值;
(2)当![]() 取何值时函数
取何值时函数![]() 的值最小?并求出
的值最小?并求出![]() 的最小值;
的最小值;
(3)设![]() (
(![]() ),且函数
),且函数![]() 与
与![]() 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数![]() 的取值范围.
的取值范围.
解:(1)∵![]() 为偶函数,故
为偶函数,故![]() 对所有
对所有![]() 都成立,(2分)即
都成立,(2分)即![]() 对所有
对所有![]() 都成立,
都成立, ![]() .(4分)
.(4分)
(2)由(1)得![]() , 即
, 即 ![]() . (2分)
. (2分)
![]() ,故当且仅当
,故当且仅当![]() 时,(3分)
时,(3分)![]() 的最小值是
的最小值是![]() .(5分)
.(5分)
(3)(理)解法1由方程![]() (
(![]() )
)
可变形为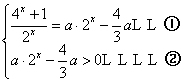 , 由②得
, 由②得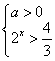 或
或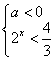 ,
,
由①得![]() ,令
,令![]() ,则
,则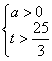 ,或
,或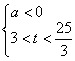
则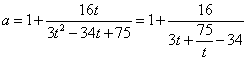 . (2分)
. (2分)
当![]() 时,
时,![]() 单调递增,∴
单调递增,∴![]() ,
,
∴![]() ,此时方程(
,此时方程(![]() )有且只有一个解; (3分)
)有且只有一个解; (3分)
当![]() 时,
时,![]() ,
,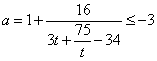
当![]() 时方程(
时方程(![]() )有且只有一个解; (4分)
)有且只有一个解; (4分)
当![]() 时,方程(
时,方程(![]() )有两解;
)有两解;
当![]() ,或
,或![]() 时方程(
时方程(![]() )无解. (5分)
)无解. (5分)
综上所述,当![]() 时,函数
时,函数![]() 与
与![]() 的图像有两个不同的公共点;
的图像有两个不同的公共点;
当![]() 或
或![]() 时,函数
时,函数![]() 与
与![]() 的图像有且只有一个公共点;
的图像有且只有一个公共点;
当![]() 或
或![]() 时,函数
时,函数![]() 与
与![]() 的图像没有公共点. (7分)
的图像没有公共点. (7分)
解法2: ![]() (
(![]() )
) 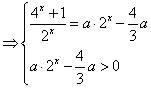
![]()
![]() (2分)
(2分)
 (3分)
(3分)
![]() (4分)
(4分)
![]() (5分)
(5分)
![]() ,
,![]() ,
,
![]() . (7分)
. (7分)
(文)由方程![]() (
(![]() )
)
可变形为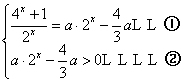 ,由②得
,由②得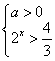 或
或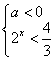 ,
,
令![]() ,则
,则![]() ,或
,或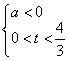
由①得![]() ,设
,设![]() (2分)
(2分)
∴当![]() 时,
时,![]() , (4分)
, (4分)
当![]() 时,
时, ![]() ,∴
,∴![]() 不存在,
不存在,
当![]() 时,
时,![]() 或
或![]() ,
,
若![]() ,则
,则![]() ,不合题意,舍去,若
,不合题意,舍去,若![]() ,则
,则![]() ,满足题意,(5分)
,满足题意,(5分)
∴当![]() 或
或![]() 时,函数
时,函数![]() 与
与![]() 的图像有且只有一个公共点. (7分)
的图像有且只有一个公共点. (7分)


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第五次联考理数 题型:解答题
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014届江苏大丰新丰中学高二上期中考试文数学试卷(解析版) 题型:解答题
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年陕西省、西工大附中高三第五次联考理数 题型:解答题
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分16分)(本题中必要时可使用公式:![]() )
)
设![]() 是各项均为正数的无穷项等差数列.
是各项均为正数的无穷项等差数列.
(Ⅰ)记![]() ,已知
,已知![]()
![]() ,试求此等差数列的首项a1及公差d;
,试求此等差数列的首项a1及公差d;
(Ⅱ)若![]() 的首项a1及公差d都是正整数,问在数列
的首项a1及公差d都是正整数,问在数列![]() 中是否包含一个非常数列
中是否包含一个非常数列
的无穷项等比数列![]() ?若存在,请写出
?若存在,请写出![]() 的构造过程;若不存在,说明理由.
的构造过程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分16分)(本题中必要时可使用公式:![]() )
)
设![]() 是各项均为正数的无穷项等差数列.
是各项均为正数的无穷项等差数列.
(Ⅰ)记![]() ,已知
,已知![]()
![]() ,试求此等差数列的首项a1及公差d;
,试求此等差数列的首项a1及公差d;
(Ⅱ)若![]() 的首项a1及公差d都是正整数,问在数列
的首项a1及公差d都是正整数,问在数列![]() 中是否包含一个非常数列
中是否包含一个非常数列
的无穷项等比数列![]() ?若存在,请写出
?若存在,请写出![]() 的构造过程;若不存在,说明理由.
的构造过程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com