
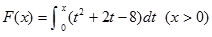 .
.
(1)求 的单调区间;(2)求函数
的单调区间;(2)求函数 在
在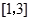 上的最值.
上的最值.
(1)单调增区间是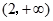 ,单调递减区间是
,单调递减区间是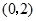 ;(2)最大值是
;(2)最大值是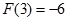 ,最小值是
,最小值是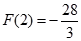 .
.
解析试题分析:(1)首先利用牛顿-莱布尼兹公式求出函数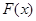 的表达式,并注意题中所给
的表达式,并注意题中所给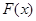 的定义域为
的定义域为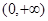 ,再利用导数通过解不等式
,再利用导数通过解不等式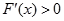 及
及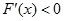 并与定义域取交集而求得函数的单调区间;(2)求函数最值的一般步骤:①求出函数在给定区间上的极值及区间的端点所对应的函数值;②比较上述值的大小;③得结论:其中最大者即为函数的最大值,最小者即为函数的最小值.
并与定义域取交集而求得函数的单调区间;(2)求函数最值的一般步骤:①求出函数在给定区间上的极值及区间的端点所对应的函数值;②比较上述值的大小;③得结论:其中最大者即为函数的最大值,最小者即为函数的最小值.
试题解析:依题意得,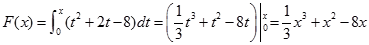 ,定义域是
,定义域是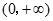 .
.
(1) ,
,
令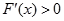 ,得
,得 或
或 ,
,
令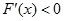 ,得
,得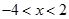
由于定义域是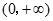 ,
, 函数的单调增区间是
函数的单调增区间是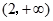 ,单调递减区间是
,单调递减区间是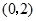 .
.
(2)令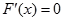 ,得
,得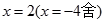 ,
,
由于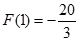 ,
,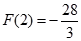 ,
,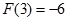 ,
,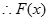 在
在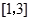 上的最大值是
上的最大值是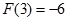 ,最小值是
,最小值是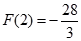 .
.
考点:1.定积分的基本公式;2.函数的单调区间;3.函数的最值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数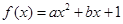 (
( 为实数,
为实数, ),
), ,⑴若
,⑴若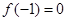 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
⑵设 ,且函数
,且函数 为偶函数,判断
为偶函数,判断 是否大0?
是否大0?
⑶设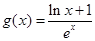 ,当
,当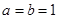 时,证明:对任意实数
时,证明:对任意实数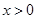 ,
, (其中
(其中 是
是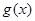 的导函数) .
的导函数) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com