
 (2)
(2)
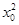 +
+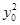 =4,
=4, =(x0,y0-1,-2),
=(x0,y0-1,-2),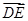 =(0,1,0),
=(0,1,0), ⊥
⊥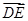 ,则
,则 ·
·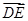 =y0-1=0,故y0=1.
=y0-1=0,故y0=1.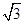 ,1,0),
,1,0), =(
=(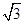 ,0,-2),
,0,-2),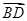 =(0,-2,2).
=(0,-2,2).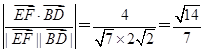 .
.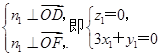
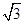 ,平面ODF的一个法向量为n1=(1,-
,平面ODF的一个法向量为n1=(1,-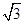 ,0).
,0).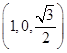 .
.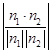 =
=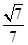 .
.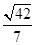 .
.

科目:高中数学 来源:不详 题型:解答题
 中,底面
中,底面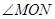 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的点.
上的点.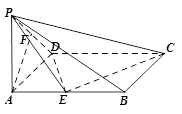
 是
是 的中点时,求证:
的中点时,求证: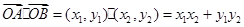 平面
平面 ;
;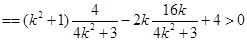 的大小为
的大小为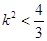 ,试确定
,试确定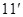 点的位置.
点的位置.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
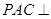 平面
平面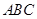 ,
,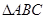 是以
是以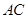 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,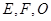 分别为
分别为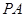 ,
,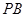 ,
,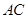 的中点,
的中点,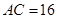 ,
,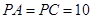 .
.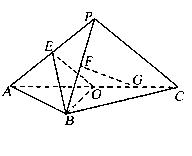
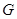 是
是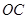 的中点,证明:
的中点,证明: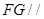 平面
平面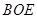 ;
;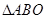 内存在一点
内存在一点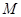 ,使
,使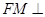 平面
平面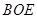 ,并求点
,并求点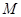 到
到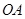 ,
,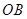 的距离.
的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
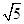 ,AB=AD=
,AB=AD=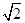 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).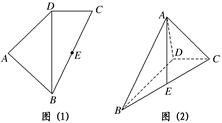
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 、
、 满足
满足 ,且
,且 与
与 的夹角为
的夹角为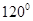 ,则
,则 在
在 上的投影等于
上的投影等于 ;
;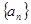 的前
的前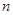 项和为
项和为 ,则
,则 、
、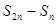 、
、 也成等比数列;
也成等比数列; 与
与 共线,则存在唯一实数
共线,则存在唯一实数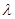 ,使得
,使得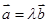 成立。
成立。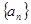 中,若
中,若 ,则
,则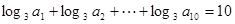
查看答案和解析>>
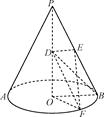
科目:高中数学 来源:不详 题型:解答题
 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com