
分析 设点A在平面BCD内的投影点为点M,可知△BCD为直角三角形,则三棱锥的外接球球心一定在过点E且垂直于平面BCD的直线上,设球心为O.单独看平面AED,如图乙,故AO=DO=R,OE=$\sqrt{{R}^{2}-1},AF=\sqrt{{R}^{2}-\frac{1}{4}}$,又EO+AF=FM+AF=AM=$\frac{\sqrt{11}}{2}$,即$\sqrt{{R}^{2}-1}+\sqrt{{R}^{2}-\frac{1}{4}}=\frac{\sqrt{11}}{2}$,解得R即可
解答 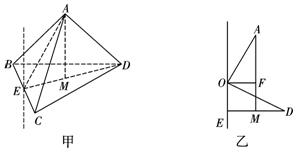 解:如图5甲所示,因为AB=AC=BC=2,∴AE=$\sqrt{3}$.
解:如图5甲所示,因为AB=AC=BC=2,∴AE=$\sqrt{3}$.
设点A在平面BCD内的投影点为点M,∵BC=2,BD=CD=$\sqrt{2}$,故△BCD为直角三角形,
∵BE=$\frac{1}{2}BC$,M为中点,∴DM=ME=$\frac{1}{2}$,故AM=$\sqrt{3-\frac{1}{4}}=\frac{\sqrt{11}}{2}$.
又因为△BCD为直角三角形,则三棱锥的外接球球心一定在过点E且垂直于平面BCD的直线上,
设球心为O.单独看平面AED,如图乙,故AO=DO=R,OE=$\sqrt{{R}^{2}-1},AF=\sqrt{{R}^{2}-\frac{1}{4}}$,
又EO+AF=FM+AF=AM=$\frac{\sqrt{11}}{2}$,即$\sqrt{{R}^{2}-1}+\sqrt{{R}^{2}-\frac{1}{4}}=\frac{\sqrt{11}}{2}$,解得R${R}^{2}=\frac{15}{11}$,
故表面积S=4$π{R}^{2}=\frac{60π}{11}$.
故答案为:$\frac{60π}{11}$
点评 本题考查球的表面积球内接多面体及其度量,考查空间想象能力,计算能力,解答的关键是根据球的性质,找到球心,求出半径,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,+∞) | C. | $({1,\root{4}{3}})$ | D. | $({\root{4}{3},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 若|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,则$\overrightarrow{a}$>$\overrightarrow{b}$ | C. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | 若|$\overrightarrow{a}$|=0,则$\overrightarrow{a}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
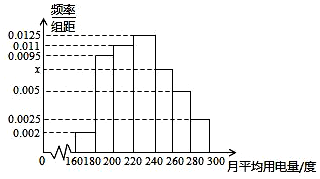 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com