
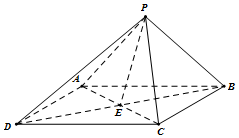
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA=PB=PC=6,∠APB=∠BPC=∠CPA=90°,AC∩BD=E.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA=PB=PC=6,∠APB=∠BPC=∠CPA=90°,AC∩BD=E.分析 (Ⅰ)推导出PB⊥面PAC,从而PB⊥AC,进而AC⊥PE,由此能证明AC⊥面PDB.
(Ⅱ)在面PAC内过E作EF⊥PA于F,则PC⊥面PAB,从而面PAC⊥面PAB,进而EF⊥面PAB,求出D到面PAC的距离等于B到面PAC的距离,由此能求出三棱锥D-AEF的体积.
解答 (本小题满分12分)
证明:(Ⅰ)因为PB⊥PA,PB⊥PC,PA∩PC=P,所以PB⊥面PAC.(2分)
又因为AC?面PAC,所以PB⊥AC.(3分)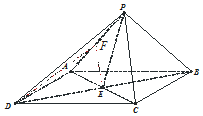
因为E是AC的中点,PA=PC,
所以AC⊥PE.(4分)
又PE∩PB=P,所以AC⊥面PDB.(5分)
解:(Ⅱ)在面PAC内过E作EF⊥PA于F,则点F为点E在面PAB的投影.(6分)
因为PC⊥PA,PC⊥PB,PA∩PB=P,所以PC⊥面PAB.(7分)
又PC?面PAC,所以面PAC⊥面PAB.(8分)
又面PAC∩面PAB=PA,EF⊥PA,所以EF⊥面PAB.(9分)
因E为AC的中点,EF∥CP,
所以F是PA的中点,${S_{△AEF}}=\frac{1}{2}×3×3=\frac{9}{2}$.(10分)
又因为E是DB的中点,
所以D到面PAC的距离等于B到面PAC的距离6,(11分)
所以三棱锥D-AEF的体积${V_{D-AEF}}=\frac{1}{3}×\frac{9}{2}×6=9$.(12分)
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{6}$,$\frac{5π}{6}$] | B. | [2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$](k∈Z) | ||
| C. | (2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$)(k∈Z) | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{5π}{6}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{n}$,$\frac{1}{m}$) | B. | ($\frac{1}{m}$,$\frac{1}{n}$) | C. | (-∞,$\frac{1}{n}$)∪($\frac{1}{m}$,+∞) | D. | (-∞,$\frac{1}{m}$)∪($\frac{1}{n}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数g(x)在区间$[{0,\frac{π}{2}}]$上单调递增 | B. | 函数f(x)与g(x)的最小正周期均为π | ||
| C. | 函数g(x)在区间$[{0,\frac{π}{2}}]$上的最大值为$\frac{{\sqrt{3}}}{2}$ | D. | 函数g(x)的对称中心为$({\frac{Kπ}{2}+\frac{π}{6},0})$(K∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com