
���� ��1������Բ���϶���ΪA����APΪֱ����Բ������ԲC���ҽ���F2��P��$\frac{4\sqrt{2}}{3}$��$\frac{b}{3}$������ԲC�ϵ�һ�㣬�г������飬���a��b���ɴ��������ԲC�ķ��̣�
��2����ֱ��l�ķ���Ϊx=my+$\sqrt{2}$����$\left\{\begin{array}{l}{x=my+\sqrt{2}}\\{{x}^{2}+2{y}^{2}=4}\end{array}\right.$����$��{m}^{2}+2��{y}^{2}+2\sqrt{2}my-2=0$���ɴ�����Τ�ﶨ������Բ���塢Ҫʹ����Բ���S���ֻ��Ҫ���F1MN�����S��������֪�����������Sȡ���ֵʱֱ��l�ķ��̣�����������ֵ��
��� �⣺��1������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����϶���ΪA����APΪֱ����Բ������ԲC���ҽ���F2��
��F2��c��0����A��0��b����P��$\frac{4\sqrt{2}}{3}��\frac{b}{3}$����
��$\overrightarrow{{F}_{2}A}•\overrightarrow{{F}_{2}P}$=��-c��b��•��$\frac{4\sqrt{2}}{3}$-c��$\frac{b}{3}$��=c2-$\frac{4\sqrt{2}}{3}c$+$\frac{{b}^{2}}{3}$=0��
��P��$\frac{4\sqrt{2}}{3}$��$\frac{b}{3}$������ԲC�ϵ�һ�㣬
��$\frac{32}{9{a}^{2}}+\frac{{b}^{2}}{9{b}^{2}}=1$�����a=2��
��a2=b2+c2�����c=$\sqrt{2}$��b=$\sqrt{2}$��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1��
��2��������ֱ��l��б�ʲ�Ϊ0����ֱ��l�ķ���Ϊx=my+$\sqrt{2}$��A��x1��y1����B��x2��y2����
��$\left\{\begin{array}{l}{x=my+\sqrt{2}}\\{{x}^{2}+2{y}^{2}=4}\end{array}\right.$����$��{m}^{2}+2��{y}^{2}+2\sqrt{2}my-2=0$��
y1+y2=$\frac{-2\sqrt{2}m}{{m}^{2}+2}$��y1y2=$\frac{-2}{{m}^{2}+2}$��
������Բ�İ뾶Ϊr����F1MN���ܳ�ΪC�����ΪS�䣬
��S��=$\frac{1}{2}Cr$��
����Բ�����C=4a=8����S��=4r��
Ҫʹ����Բ���S���ֻ��Ҫ���F1MN�����S�����
��F1MN�������
S��=$\frac{1}{2}��2c��|{y}_{1}-{y}_{2}|$=$\sqrt{2}\sqrt{��{y}_{1}+{y}_{2}��^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{2[��\frac{-2\sqrt{2}m}{{m}^{2}+2}��^{2}-4•\frac{-2}{{m}^{2}+2}]}$=$\frac{4\sqrt{2}•\sqrt{{m}^{2}+1}}{{m}^{2}+2}$��
��t=$\sqrt{{m}^{2}+1}$��t��1��
S��=$\frac{4\sqrt{2}t}{{t}^{2}+1}$=$\frac{4\sqrt{2}}{t+\frac{1}{t}}$$��2\sqrt{2}$��
���ҽ���t=1����m=0ʱȡ�Ⱥţ�
��ʱr=$\frac{\sqrt{2}}{2}$��S=��r2=$\frac{��}{2}$��
ֱ��l�ķ���Ϊx=$\sqrt{2}$��
���� ���⿼����Բ���̵������鵱�����ε�����Բ�����ȡ���ֵʱֱ��l�ķ��̼�������ֵ�������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ�����ҳ���ʽ���㵽ֱ�߾��빫ʽ����Բ���ʵĺ������ã�


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
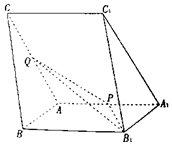 ��ͼ��������ABC-A1B1C1�У���B1A1A=��C1A1A=60�㣬AA1=AC=4��AB=2��P��Q�ֱ�Ϊ��AA1��AC���е㣮
��ͼ��������ABC-A1B1C1�У���B1A1A=��C1A1A=60�㣬AA1=AC=4��AB=2��P��Q�ֱ�Ϊ��AA1��AC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��+�ޣ� | B�� | ��2��5] | C�� | ��1��2�� | D�� | ��1��5] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��0�� | B�� | ��-1��0�� | C�� | ��-1��1�� | D�� | ��0��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com