
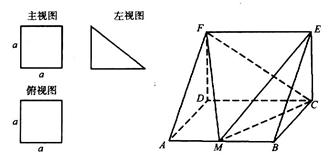
 的三视图如图所示.
的三视图如图所示.
 是直角三角形;
是直角三角形; 求三棱锥
求三棱锥 是全面积;
是全面积; 在线段
在线段 上何处时,
上何处时, 与平面
与平面 所成的角为
所成的角为 .
.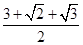
 为线段
为线段 的中点时,
的中点时, 与平面
与平面 所成的角为
所成的角为
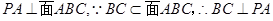
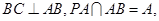

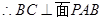 ,
,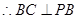
 是以
是以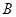 为直角顶点的直角三角形. 4分
为直角顶点的直角三角形. 4分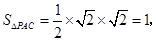 且
且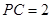
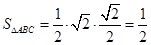 ,
,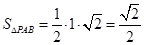 ,且
,且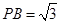
 是直角三角形,故其面积为
是直角三角形,故其面积为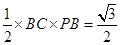
 的全面积为
的全面积为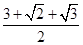 8分
8分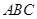 内过
内过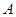 做
做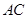 的垂线
的垂线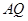 ,
,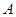 为原点,
为原点, 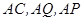 所在直线分别为
所在直线分别为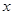 轴、
轴、 轴 、
轴 、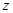 轴建立空间直角坐标系,如图所示
轴建立空间直角坐标系,如图所示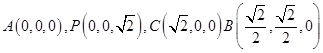
 为面
为面 的一个法向量,
的一个法向量,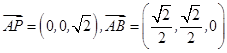
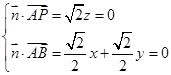
 取
取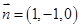
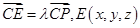 ,
,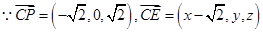 ,
,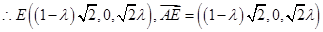
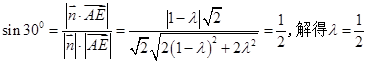
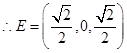 ,故当
,故当 为线段
为线段 的中点时,
的中点时, 与平面
与平面 所成的角为
所成的角为 ……13分
……13分 ×底面积×高.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”,三视图是新课标的新增内容,在以后的高考中有加强的可能.用向量法求线面角是空间向量的一个重要运用,其步骤是:一、建立坐标系,表示出相应量的坐标,二、求出直线的方向向量以及面的法向量,三、利用公式表示线面角或者面面角的三角函数值求角.用向量解决几何问题是新课标的新增内容,这几年高考中此工具是一个常考常新的类型.
×底面积×高.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”,三视图是新课标的新增内容,在以后的高考中有加强的可能.用向量法求线面角是空间向量的一个重要运用,其步骤是:一、建立坐标系,表示出相应量的坐标,二、求出直线的方向向量以及面的法向量,三、利用公式表示线面角或者面面角的三角函数值求角.用向量解决几何问题是新课标的新增内容,这几年高考中此工具是一个常考常新的类型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
A.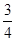 | B.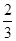 | C.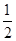 | D.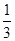 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com