
【题目】2018年元旦期间,某运动服装专卖店举办了一次有奖促销活动,消费每超过400元均可参加1次抽奖活动,抽奖方案有两种,顾客只能选择其中的一种.
方案一:顾客转动十二等分且质地均匀的圆形转盘(如图),转盘停止转动时指针指向哪个扇形区域,则顾客可直接获得该区域对应面额(单位:元)的现金优惠,且允许顾客转动3次.
方案二:顾客转动十二等分且质地均匀的圆形转盘(如图〕,转盘停止转动时指针若指向阴影部分,则未中奖,若指向白色区域,则顾客可直接获得40元现金,且允许顾客转动3次.

(1)若两位顾客均获得1次抽奖机会,且都选择抽奖方案一,试求这两位顾客均获得180元现金优惠的概率;
(2)若某顾客恰好获得1次抽奖机会.
①试分别计算他选择两种抽奖方案最终获得现金奖励的数学期望;
②从概率的角度比较①中该顾客选择哪一种抽奖方案更合算?
【答案】(1) ![]() (2) ①见解析②该顾客选择第一种抽奖方案更合算
(2) ①见解析②该顾客选择第一种抽奖方案更合算
【解析】试题分析:(1)由图可知,每一次转盘指向60元对应区域的概率为![]() ,设“每位顾客获得180元现金奖励”为事件
,设“每位顾客获得180元现金奖励”为事件![]() ,则
,则![]() ,结合乘法概率公式得到这两位顾客均获得180元现金优惠的概率;
,结合乘法概率公式得到这两位顾客均获得180元现金优惠的概率;
(2)①方案一: ![]() 可能的取值为60,100,140,180,
可能的取值为60,100,140,180, ![]() 方案二:
方案二: ![]() ,故
,故![]() ;
;
②由①知![]() ,所以该顾客选择第一种抽奖方案更合算.
,所以该顾客选择第一种抽奖方案更合算.
试题解析:
(1)选择方案一,若要享受到180元的现金优惠,则必须每次旋转转盘都指向60元对应的区域, 由图可知,每一次转盘指向60元对应区域的概率为![]() .
.
设“每位顾客获得180元现金奖励”为事件![]() ,
,
则![]() ,
,
所以两位顾客均获得180元现金奖励的概率为![]() .
.
(2)①若选择抽奖方案一,则每一次转盘指向60元对应区域的概率为![]() ,每一次转盘指向20元对应区域的概率为
,每一次转盘指向20元对应区域的概率为![]() .
.
设获得现金奖励金额为![]() 元,
元,
则![]() 可能的取值为60,100,140,180.
可能的取值为60,100,140,180.
则![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
所以选择抽奖方案一,该顾客获得现金奖励金额的数学期望为![]() (元).
(元).
若选择抽奖方案二,设三次转动转盘的过程中,指针指向白色区域的次数为![]() ,最终获得现金奖励金额为
,最终获得现金奖励金额为![]() 元,则
元,则![]() ,故
,故![]() ,
,
所以选择抽奖方案二,该顾客获得现金奖励金额的数学期望为![]() (元).
(元).
②由①知![]() ,
,
所以该顾客选择第一种抽奖方案更合算.


科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
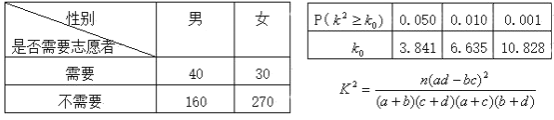
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在过点![]() 的直线
的直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() ,满足
,满足![]() ?
?
若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,对任意n∈N*总有2Sn=an2+n,且an<an+1.若对任意n∈N*,θ∈R,不等式![]() λ(n+2)恒成立,求实数λ的最小值( )
λ(n+2)恒成立,求实数λ的最小值( )
A.1![]() B.2C.1D.
B.2C.1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若数列![]() 的通项公式分别为
的通项公式分别为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() (
(![]() 是不为零的常数),求证:数列
是不为零的常数),求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() (
(![]() 为常数,
为常数,![]() ),
),![]() (
(![]() ,
,![]() ),对任意
),对任意![]() ,
,![]() ,求出数列
,求出数列![]() 的最大项(用含
的最大项(用含![]() 式子表达).
式子表达).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·沧州质检]对于椭圆![]() ,有如下性质:若点
,有如下性质:若点![]() 是椭圆上的点,则椭圆在该点处的切线方程为
是椭圆上的点,则椭圆在该点处的切线方程为![]() .利用此结论解答下列问题.点
.利用此结论解答下列问题.点![]() 是椭圆
是椭圆![]() 上的点,并且椭圆在点
上的点,并且椭圆在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若动点![]() 在直线
在直线![]() 上,经过点
上,经过点![]() 的直线
的直线![]() ,
,![]() 与椭圆
与椭圆![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() .求证:直线
.求证:直线![]() 必经过一定点.
必经过一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com