练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求由曲线y=x2与y=2-x2所围成图形的面积为    ．
    【答案】分析：作出两个曲线的图象并求出它们的交点坐标．利用定积分公式并结合函数图象的对称性，可得所求面积为函数  2-2x2在区间[0，1]上的定积分值的2倍，再加以运算即可得到本题答案．
    解答：解：∵曲线y=x2和曲线y=2-x2所的交点为（1，1）和（-1，1）
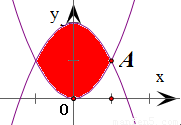
    ∴曲线y=x2和曲线y=2-x2所围图形的面积为
    S=2=2
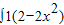
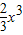
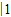
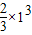
    =2（2x-）=2[（2×1-）-（2×0-）]=
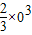
    故答案为：
    点评：本题求两条曲线围成的曲边图形的面积，着重考查了定积分的几何意义和积分计算公式等知识，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    求由曲线y=x2与y=2-x2所围成图形的面积为
    8
    3
    8
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：解答题

    求由曲线y=x2与直线x+y=2围成的图形的面积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求由曲线y=x2与直线x+y=2围成的面积.?

          

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求由曲线y = x2 与 y = 2- x2 围成的平面图形的面积.

    查看答案和解析>>

    同步练习册答案