
分析 (1)由题意和余弦定理求出cosA的值,由内角的范围和特殊角的三角函数值求出A;
(2)在ABC中由题意和余弦定理表示出a2,化简后得b2+c2=bc+3,由重要不等式得bc≤3,由余弦定理表示出cosB,在ABM中由余弦定理表示出AM2,化简后可求出AM的最大值.
解答 解:(1)因为b2+c2-a2=bc,
所以cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
由0°<A<180°得A=60°;
(2)在ABC中,A=60°,a=$\sqrt{3}$,
由余弦定理得,a2=b2+c2-2bccosA,
化简得,b2+c2-bc=3,则b2+c2=bc+3,
且b2+c2=bc+3≥2bc,得bc≤3,(当且仅当b=c时取等号)
在ABC中,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
在ABM中,M是BC的中点,由余弦定理得,
AM2=AB2+BM2-2•AB•BM•cosB
=c2+$\frac{{a}^{2}}{4}$-2•c•$\frac{1}{2}a$•$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$
=$\frac{{2c}^{2}+2{b}^{2}-{a}^{2}}{4}$=$\frac{2(bc+3)-3}{4}$
=$\frac{2bc+3}{4}≤\frac{9}{4}$,则AM≤$\frac{3}{2}$,
所以中线AM的最大值是$\frac{3}{2}$.
点评 本题考查余弦定理,以及重要不等式在求最值中的应用,考查化简、变形能力.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
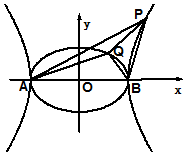 已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )
已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )| A. | 大于0 | B. | 等于0 | ||
| C. | 小于0 | D. | 大于0,等于0,小于0都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{12}$ | C. | $\frac{7\sqrt{3}}{12}$ | D. | -$\frac{7\sqrt{3}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
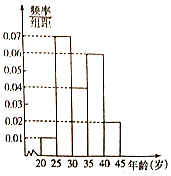 今年我国许多省市雾霾频发,为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组:第一组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
今年我国许多省市雾霾频发,为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组:第一组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
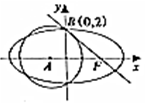 如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.
如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com