Question

20．在平面直角坐标系中，圆心坐标均为（2，2）的圆Ⅰ、圆Ⅱ、圆Ⅲ半径分别为4，2，1，直线y=$\frac{3}{4}$x+3与圆Ⅰ交于点A，B，点C在圆Ⅰ上，满足线段CA和线段CB与圆Ⅱ均有公共点，点P是圆Ⅲ上任意一点，则△APB与△APC面积之比的最大值为$\frac{3+\sqrt{5}}{2}$．

Answer 1

分析 根据三角形的面积公式判断出两个面积的比值最大时，角∠BAP应达到最大，根据图象确定此时点P的位置，再由条件列出角之间的关系，表示出两个三角形的面积的比值的表达式，由角大小关系列出面积比值的不等式：$\frac{{S}_{△APB}}{{S}_{△APC}}$≤$\frac{sin（\frac{π}{6}+θ）}{sin（\frac{π}{6}-β）}$，再根据三角形有关的数据求出角的三角函数值，利用两角和差的正弦公式求出$\frac{sin（\frac{π}{6}+θ）}{sin（\frac{π}{6}-β）}$的值即可．

解答 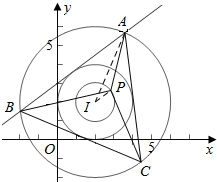解：由题意可得|PI|=1知，点P在以I为圆心的单位圆上，
设∠BAP=α，假设点P使α达到最大值β，此时点P应落在∠IAP内，
且此时AP应与单位圆I相切，
由弦长公式可得AB=2$\sqrt{{4}^{2}-（\frac{3×2-4×2+12}{5}）^{2}}$=4$\sqrt{3}$，
再由线段CA和线段CB与圆Ⅱ均有公共点，可得△ABC是等边三角形，
所以0＜α≤β＜$\frac{π}{3}$，
令∠IAP=θ，则θ=$β-\frac{π}{6}$，所以β=$\frac{π}{6}$+θ，
则$\frac{{S}_{△APB}}{{S}_{△APC}}$=$\frac{\frac{1}{2}AP•ABsinα}{\frac{1}{2}AP•ACsin（\frac{π}{3}-α）}$=$\frac{sinα}{sin（\frac{π}{3}-α）}$≤$\frac{sinβ}{sin（\frac{π}{3}-β）}$=$\frac{sin（\frac{π}{6}+θ）}{sin（\frac{π}{6}-β）}$，①
因为等边三角形ABC的边长为4$\sqrt{3}$，其重心（中线交点）为I，所以AI=4，
由∠API=90°得，sinθ=$\frac{IP}{AI}$=$\frac{1}{4}$，则cosθ=$\sqrt{1-si{n}^{2}θ}$=$\frac{\sqrt{15}}{4}$，
即tanθ=$\frac{\sqrt{15}}{15}$，
所以$\frac{sin（\frac{π}{6}+θ）}{sin（\frac{π}{6}-β）}$=$\frac{\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ}{\frac{1}{2}cosθ-\frac{\sqrt{3}}{2}sinθ}$=$\frac{\frac{1}{2}+\frac{\sqrt{3}}{2}tanθ}{\frac{1}{2}-\frac{\sqrt{3}}{2}tanθ}$=$\frac{1+\sqrt{3}×\frac{\sqrt{15}}{15}}{1-\sqrt{3}×\frac{\sqrt{15}}{15}}$=$\frac{3+\sqrt{15}}{2}$，②
由①②知，当AP与单位圆I相切时，
$\frac{{S}_{△APB}}{{S}_{△APC}}$的值达到最大，最大值为：$\frac{3+\sqrt{5}}{2}$．
故答案为：$\frac{3+\sqrt{5}}{2}$．

点评 本题以等边三角形为载体考查了最值问题，平面几何的知识，以及两角和差的正弦公式，关键是利用三角形的面积公式，判断出两个面积的比值最大时对应的条件，难度较大，考查分析问题、解决问题的能力，需要较强的逻辑分析能力．