
【题目】函数y=loga(x+3)﹣1(a>0且a≠1)的图象恒过定点A,若点A在mx+ny+2=0上,其中mn>0,则 ![]() 的最小值为 .
的最小值为 .
【答案】4
【解析】解:∵函数y=loga(x+3)﹣1(a>0且a≠1)的图象恒过定点A,
∴x+3=1,x=﹣2,y=﹣1.即A(﹣2,﹣1).
∵点A在mx+ny+2=0上,
∴﹣2m﹣n+2=0,即2m+n=2,又mn>0,
∴m>0,n>0,
∴ ![]() =
= ![]() (
( ![]() )(2m+n)=
)(2m+n)= ![]() [2+
[2+ ![]() +
+ ![]() +2]≥
+2]≥ ![]() (4+4)=4(当且仅当n=2m=1,即m
(4+4)=4(当且仅当n=2m=1,即m ![]() ,n=1时取“=”)
,n=1时取“=”)
所以答案是:4.
【考点精析】通过灵活运用对数函数的单调性与特殊点和基本不等式,掌握过定点(1,0),即x=1时,y=0;a>1时在(0,+∞)上是增函数;0>a>1时在(0,+∞)上是减函数;基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知四边形ABCD内接于圆O
(1)若AB=2,BC=6,CD=4,AC=8,求BD
(2)若AC=![]() ,BC=
,BC=![]() +1,∠ADB=
+1,∠ADB=![]() ,求AD2+DC2的取值范围
,求AD2+DC2的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心M在y轴上,半径为1.直线l:y=2x+2被圆M所截得的弦长为 ![]() ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.
(1)求圆M的方程;
(2)设A(t,0),B(t+5,0)(﹣4≤t≤﹣1),若AC,BC是圆M的切线,求△ABC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器﹣﹣﹣雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
若降尘率达到18%以上,则认定雾炮除尘有效.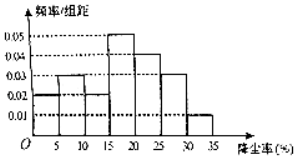
(1)根据以上数据估计雾炮除尘有效的概率;
(2)现把A市规划成三个区域,每个区域投放3台雾炮进行除尘(雾炮之间工作互不影响),若在一个区域内的3台雾炮降尘率都低于18%,则需对该区域后期追加投入20万元继续进行治理,求后期投入费用的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,过点P(2,1)的直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,已知直线l与曲线C交于A、B两点.
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,已知直线l与曲线C交于A、B两点.
(1)求曲线C的直角坐标方程;
(2)求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】锐角△ABC中,角A、B、C所对的边分别为a、b、c,且tanA﹣tanB= ![]() (1+tanAtanB).
(1+tanAtanB).
(Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(Ⅱ)已知向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),求|3
=(cosB,sinB),求|3 ![]() ﹣2
﹣2 ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若 ![]() =t
=t ![]() .
. 
(1)当t= ![]() 时,求证:平面SAE⊥平面MNPQ;
时,求证:平面SAE⊥平面MNPQ;
(2)是否存在实数t,使得二面角M﹣PQ﹣A的平面角的余弦值为 ![]() ?若存在,求出实数t的值;若不存在,说明理由.
?若存在,求出实数t的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com