
【题目】已知函数f(x)=|ax-2|+lnx(其中a为常数)
(1)若a=0,求函数g(x)=![]() 的极值;
的极值;
(2)求函数f(x)的单调区间;
(3)令F(x)=f(x)-![]() ,当a≥2时,判断函数F(x)在(0,1]上零点的个数,并说明理由.
,当a≥2时,判断函数F(x)在(0,1]上零点的个数,并说明理由.
【答案】(1)极大值为e,无极小值.(2)见解析(3)见解析
【解析】
(1)直接利用导数求函数的极值;(2)对a分a≤0和a>0两种情况讨论,利用导数求函数的单调区间;(3)由题得|ax-2|=![]() -lnx,先求出函数y=
-lnx,先求出函数y=![]() -lnx在(0,1]上为减函数,函数的最小值为y=1,再对a分类讨论,结合数形结合分析得到函数F(x)在(0,1]上零点的个数.
-lnx在(0,1]上为减函数,函数的最小值为y=1,再对a分类讨论,结合数形结合分析得到函数F(x)在(0,1]上零点的个数.
解:(1)当a=0时,f(x)=2+lnx,
g(x)=![]() ,g'(x)=-
,g'(x)=-![]() ,由g'(x)=0,得x=
,由g'(x)=0,得x=![]() ,
,
当0<x<![]() 时,g′(x)>0 g(x)单调递增:
时,g′(x)>0 g(x)单调递增:
当x>![]() 时,g′(x)<0,g(x)单调递减,即当x=
时,g′(x)<0,g(x)单调递减,即当x=![]() ,时函数g(x)取得极大值,极大值为g(
,时函数g(x)取得极大值,极大值为g(![]() )=e,无极小值.
)=e,无极小值.
(2)若a≤0.则f(x)=-ax+2+lnx,f′(x)=-a+![]() >0,
>0,
∴f(x)在(0,+∞)上单调递增,
若a>0,则f(x)=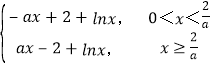 ,
,
当x≥![]() 时,f′(x)=a+
时,f′(x)=a+![]() >0,∴f(x)在[
>0,∴f(x)在[![]() ,+∞)上单调递增,
,+∞)上单调递增,
当0<x<![]() 时,f′(x)=-a+
时,f′(x)=-a+![]() ,
,
由f′(x)>0得0<x<![]() ,此时函数单调递增,
,此时函数单调递增,
由f′(x)<0得![]() <x<
<x<![]() ,此时函数单调递减,
,此时函数单调递减,
综上当a≤0时,f(x)的单调递增区间为(0,+∞),
当a>0时,f(x)的单调递增区间为(0,![]() ),[
),[![]() ,+∞),单调递减区间为(
,+∞),单调递减区间为(![]() ,
,![]() ).
).
(3)F(x)=f(x)-![]() =|ax-2|+lnx-
=|ax-2|+lnx-![]() ,
,
由F(x)=0得|ax-2|=![]() -lnx,
-lnx,
则k(x)=![]() -lnx,则函数在(0,1]上为减函数,函数的最小值为y=1,
-lnx,则函数在(0,1]上为减函数,函数的最小值为y=1,
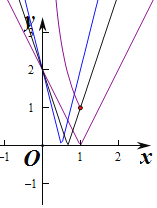
当![]() 时,y=|ax-2|的零点为
时,y=|ax-2|的零点为![]() ∈(0,1],
∈(0,1],
当x![]() 时,F(x)=f(x)-
时,F(x)=f(x)-![]() =|ax-2|+lnx
=|ax-2|+lnx![]() ,
,
由F(x)=0,得![]() ,即
,即![]() .
.
令![]() ,
,![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,![]() ,又
,又![]() ,所以
,所以![]() 时
时![]() ,
,
因为![]() ,所以
,所以![]() 时F(x)无零点.
时F(x)无零点.
当x≥![]() 时,y=ax-2,设h(x)=ax-2,
时,y=ax-2,设h(x)=ax-2,
当h(1)≥1.即a-2≥1,即a≥3时,两个函数有1个交点,即函数F(x)在(0,1]上零点的个数为1个,
当h(1)<1.即a-2<1,即2<a<3时,两个函数有0个交点,即函数F(x)在(0,1]上零点的个数为0个,
综合得2≤a<3时,函数F(x)在(0,1]上零点的个数为0个,a≥3时,函数F(x)在(0,1]上零点的个数为1个,


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 (其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(Ⅰ)写出直线l普通方程和曲线C的直角坐标方程;
(Ⅱ)过点M(-1,0)且与直线l平行的直线l1交C于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假:
(1)![]() 是有理数;(2)
是有理数;(2)![]() ;
;
(3)奇数的平方仍是奇数;(4)两个集合的交集还是一个集合;
(5)每一个素数都是奇数;(6)方程![]() 有实数根;
有实数根;
(7)![]() ;(8)如果
;(8)如果![]() ,那么
,那么![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 且
且![]() .圆C与直线
.圆C与直线![]() 相切于点A,且点A的纵坐标为
相切于点A,且点A的纵坐标为![]() ,圆心C在直线
,圆心C在直线![]() 上.
上.
(1)求直线![]() 之间的距离;
之间的距离;
(2)求圆C的标准方程;
(3)若直线![]() 经过点
经过点![]() 且与圆C交于
且与圆C交于![]() 两点,当△CPQ的面积最大时,求直线
两点,当△CPQ的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班共有学生45人,其中女生18人,现用分层抽样的方法,从男、女学生中各抽取若干学生进行演讲比赛,有关数据见下表(单位:人)
性别 | 学生人数 | 抽取人数 |
女生 | 18 |
|
男生 |
| 3 |
(1)求![]() 和
和![]() ;
;
(2)若从抽取的学生中再选2人做专题演讲,求这2人都是男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
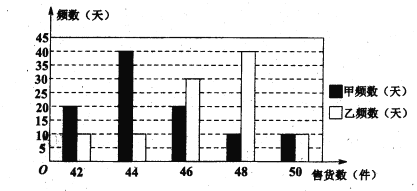
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】(I)见解析; (Ⅱ)见解析.
【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.
详解:(I)由题意得,甲公司一名推销员的日工资![]() (单位:元) 与销售件数
(单位:元) 与销售件数![]() 的关系式为:
的关系式为: ![]() .
.
乙公司一名推销员的日工资![]() (单位: 元) 与销售件数
(单位: 元) 与销售件数![]() 的关系式为:
的关系式为: 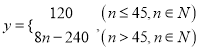
(Ⅱ)记甲公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
记乙公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴仅从日均收入的角度考虑,我会选择去乙公司.
点睛:求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值
【题型】解答题
【结束】
19
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
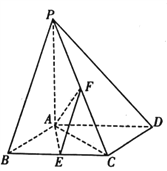
(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x+ax2-2x,(a∈R,a≠0)
(1)若函数f(x)的图象在x=1处的切线与x轴平行,求f(x)的单调区间;
(2)若f(x)≤ax在x∈[![]() ,+∞)上恒成立,求a的取值范围.
,+∞)上恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com