
【题目】在等差数列{an}中,a3+a4=12,公差d=2,记数列{a2n﹣1}的前n项和为Sn .
(1)求Sn;
(2)设数列{ ![]() }的前n项和为Tn , 若a2 , a5 , am成等比数列,求Tm .
}的前n项和为Tn , 若a2 , a5 , am成等比数列,求Tm .
【答案】
(1)解:∵在等差数列{an}中,a3+a4=12,公差d=2,
∴(a1+2×2)+(a1+3×2)=12,
解得a1=1,
∴an=1+(n﹣1)×2=2n﹣1.
∵数列{a2n﹣1}的前n项和为Sn,
a2n﹣1=2(2n﹣1)﹣1=4n﹣3,
∴{a2n﹣1}是1为首项,4为公差的等差数列,
∴ ![]() =2n2﹣n.
=2n2﹣n.
(2)∵a2,a5,am成等比数列,∴ ![]() ,
,
∴3(2m﹣1)=92,
解得m=14.
∵ ![]() =
= ![]() =
= ![]() (
( ![]() ),
),
∴Tm=T14= ![]() (1﹣
(1﹣ ![]() +…+
+…+ ![]() )
)
= ![]() =
= ![]() .
.
【解析】(1)根据等差数列的性质,结合a3+a4=12可得到a1=1,不难写出an的通项公式,再表示出a2n﹣1的通项公式,可知道其为等差数列,再根据等差数列前n项和可得结果,(2)由a2,a5,am成等比数列可得![]() ,解出m=14,再表示出Tm,裂项求和可得Tm的值.
,解出m=14,再表示出Tm,裂项求和可得Tm的值.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系 ).
).


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,右顶点为E,P为直线x=
,右焦点为F,右顶点为E,P为直线x= ![]() a上的任意一点,且(
a上的任意一点,且( ![]() +
+ ![]() )
) ![]() =2.
=2.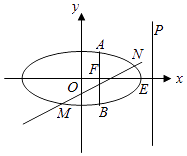
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F垂直于x轴的直线AB与椭圆交于A,B两点(点A在第一象限),动直线l与椭圆C交于M,N两点,且M,N位于直线AB的两侧,若始终保持∠MAB=∠NAB,求证:直线MN的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是公差为d(d≠0)的等差数列,Sn为其前n项和,a1 , a2 , a5成等比数列.
(Ⅰ)证明S1 , S3 , S9成等比数列;
(Ⅱ)设a1=1,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合U={1,2,…,100},TU.对数列{an}(n∈N*),规定:
①若T=,则ST=0;
②若T={n1 , n2 , …,nk},则ST=a ![]() +a
+a ![]() +…+a
+…+a ![]() .
.
例如:当an=2n,T={1,3,5}时,ST=a1+a3+a5=2+6+10=18.
已知等比数列{an}(n∈N*),a1=1,且当T={2,3}时,ST=12,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,左焦点为F(﹣1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
,左焦点为F(﹣1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
(1)求椭圆C的标准方程;
(2)在y轴上,是否存在定点E,使 ![]() 恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C的极坐标方程为ρ=2cosθ+2sinθ(0≤θ<2π),点M(1, ![]() ),以极点O为原点,以极轴为x轴的正半轴建立平面直角坐标系.已知直线l:
),以极点O为原点,以极轴为x轴的正半轴建立平面直角坐标系.已知直线l: 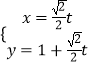 (t为参数)与曲线C交于A,B两点,且|MA|>|MB|.
(t为参数)与曲线C交于A,B两点,且|MA|>|MB|.
(1)若P(ρ,θ)为曲线C上任意一点,求ρ的最大值,并求此时点P的极坐标;
(2)求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.
(1)证明:平面ACP⊥平面ABC;
(2)若E为棱PB与P不重合的点,且AE⊥CE,求AE与平面ABC所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】所谓正三棱锥,指的是底面为正三角形,顶点在底面上的射影为底面三角形中心的三棱锥,在正三棱锥 ![]() 中,
中, ![]() 是
是 ![]() 的中点,且
的中点,且 ![]() ,底面边长
,底面边长 ![]() ,则正三棱锥
,则正三棱锥 ![]() 的体积为 , 其外接球的表面积为 .
的体积为 , 其外接球的表面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com