
分析 (1)方法一:由题意可知原不等式可知转化成,h(x)max≤-1,由g(1)+1≤0,求得a≥1,由当a≥1时,h'(x)=0,即可求得x=1,x=-1+$\frac{1}{a}$,利用导数与函数单调性关系,即可求得实数a的取值范围;
方法二:分类,根据a的取值范围,利用导数与函数单调性的关系,分别解得x的取值范围,即可求得实数a的取值范围;
(2)由ln(1+x)≤x,x>-1,则(1+x ) ${\;}^{\frac{1}{x}}$<e,则$(1+x)^{\frac{1}{x}}$<e,1,$\frac{1}{2}$,$\frac{1}{3}$,…,$\frac{1}{n}$ (n∈N*)代换x,2<e,( $\frac{3}{2}$)2<e,( $\frac{4}{3}$)3<e,…( $\frac{n+1}{n}$)n<e,累乘法,即可求得n+1<e$\root{n}{n!}$.
解答 解:(1)方法一:令h(x)=lnx-f(x),则h(x)=lnx-f(x)≤-1,
即ln-(ax+$\frac{a-1}{x}$)≤-1恒成立,g(x)≤-1恒成立即g(x)max≤-1.
则g(1)+1=-a-a+1+1≤0,解得:a≥1,
而当a≥1时,h'(x)=$\frac{-(ax+a-1)(x-1)}{{x}^{2}}$=0,解得:x=1,x=-1+,4分
x=-1+$\frac{1}{a}$≤0,则x∈(0,1),h'(x)>0,h(x)在(0,1)单调递增,
当x∈(1,+∞),h'(x)<0,h(x)在(1,+∞)单调递减,
则h(x)max=g(1)=1-2a≤-1,与题意相符,
即h(x)≤-1恒成立,实数a的取值范围为a≥1;
方法二:h'(x)=$\frac{1}{x}$-a+$\frac{a-1}{{x}^{2}}$=$\frac{-a{x}^{2}+x+a-1}{{x}^{2}}$=$\frac{-(ax+a-1)(x-1)}{{x}^{2}}$,2分
(1)当a=0时,g'(x)=$\frac{x-1}{{x}^{2}}$,x∈(0,1),h'(x)<0,
h(x)在(0,1)单调递减,当x∈(1,+∞),h'(x)>0,h(x)在(1,+∞)单调递增.
则h(x)min=g(1)=1,与题意不符;
(2)当a≠0时,h'(x)=$\frac{-(ax+a-1)(x-1)}{{x}^{2}}$=$\frac{-a[x-(-1+\frac{1}{a})(x-1)]}{{x}^{2}}$=0,解得:x=1,x=-1+$\frac{1}{a}$,
①若a<0,-1+$\frac{1}{a}$<0,x∈(0,1),h'(x)<0,h(x)单调递减;
当x∈(1,+∞),h'(x)>0,h(x)单调递增,则h(x)max=h(1)=1-2a<-1,则a>1,矛盾,
与题意不符; 4分
②若a>0,
(ⅰ)若0<a<$\frac{1}{2}$,-1+$\frac{1}{a}$>1,x∈(0,1),g'(x)<0;
x∈(1,-1+$\frac{1}{a}$),h'(x)>0;
x∈(-1+$\frac{1}{a}$,+∞),h'(x)<0,
∴h(x)在(0,1)单调递减,h(x)在(1,-1+$\frac{1}{a}$)单调递增,h(x)在(-1+$\frac{1}{a}$,+∞)单调递减,
h(1)=1-2a>0与题意不符;
(ⅱ)若a=$\frac{1}{2}$时,x∈(0,+∞),g'(x)≤0,
∴h(x)在(0,+∞)单调递减,h(1)=1-2a=0,与题意不符.
(ⅲ)若$\frac{1}{a}$<a<1,0<-1+$\frac{1}{a}$<1,x∈(0,-1+$\frac{1}{a}$),h'(x)<0,x∈(-1+$\frac{1}{a}$,1),h'(x)>0,x∈(1,+∞),h'(x)<0,
h(x)在(0,-1+$\frac{1}{a}$)单调递减,在(-1+$\frac{1}{a}$,1)单调递增,在(1,+∞)单调递减,h(1)=1-2a>-1,与已知矛盾不符题意.
(ⅳ)若a≥1,-1+$\frac{1}{a}$≤0,x∈(0,1),h'(x)>0,h(x)在(0,1)单调递增;
当x∈(1,+∞),h'(x)<0,h(x)在(1,+∞)单调递减,则h(x)>h(1)=1-2a≤-1,与题意相符;
综上,得h(x)≤-1恒成立,实数a的取值范围为a≥1;
(2)证明:由(1)知,当a=1时,有lnx≤x-1,x>0;于是有ln(1+x)≤x,x>-1,8分
则当x>0时,有$\frac{1}{x}$ln(1+x)<1,则$ln(x+1)^{\frac{1}{x}}$<1,$(1+x)^{\frac{1}{x}}$<e,10分
在上式中,用1,$\frac{1}{2}$,$\frac{1}{3}$,…,$\frac{1}{n}$ (n∈N*)代换x,
可得2<e,( $\frac{3}{2}$)2<e,( $\frac{4}{3}$)3<e,…( $\frac{n+1}{n}$)n<e相乘得 $\frac{(n+1)!}{n!}$<en,n+1<e$\root{n}{n!}$.
∴n+1<e$\root{n}{n!}$.
点评 本题考查导数的综合应用,考查利用导数求函数的单调性及最值,考查分类讨论思想,属于难题.


科目:高中数学 来源: 题型:解答题
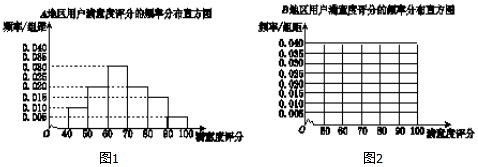
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 14 | 10 | 6 |
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\root{3}{{\frac{9}{2e}}}$ | B. | $\frac{1}{6}\root{3}{{\frac{1}{6e}}}$ | C. | $\frac{1}{9}\root{3}{{\frac{{4{e^2}}}{3}}}$ | D. | 以上答案均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A与B | B. | B与C | C. | A与D | D. | C与D |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,0) | B. | [-3,0] | C. | (0,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=2n-1 | B. | an=3n | C. | 2 | D. | an=5n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
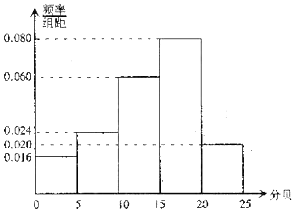 人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com