
【题目】已知函数f(1﹣ ![]() )的定义域为[1,+∞),则函数y=
)的定义域为[1,+∞),则函数y= ![]() 的定义域为 .
的定义域为 .
科目:高中数学 来源: 题型:
【题目】如图,在凸四边形ABCD中,AB=1,BC= ![]() ,AC⊥DC,CD=
,AC⊥DC,CD= ![]() AC.设∠ABC=θ.
AC.设∠ABC=θ. 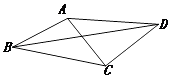
(1)若θ=30°,求AD的长;
(2)当θ变化时,求BD的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 平面ABC.
平面ABC.
![]() 若
若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
![]() 在
在![]() 的条件下,求二面角
的条件下,求二面角![]() 的大小;
的大小;
![]() 若
若![]() ,
,![]() 平面
平面![]() ,G为垂足,令
,G为垂足,令![]() 其中p、q、
其中p、q、![]() ,求p、q、r的值.
,求p、q、r的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a、b、c,a=btanA,且B为钝角.
(1)证明:B﹣A= ![]() ;
;
(2)求sinA+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣1,其中n∈N* .
(1)求数列{an}的通项公式;
(2)设anbn= ![]() ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为定义域
为定义域![]() 上的奇函数,且在
上的奇函数,且在![]() 上是单调递增函数,函数
上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,
为等差数列,![]() ,且公差不为0,若
,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45 B. 15 C. 10 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有两台不同机器A和B生产同一种产品各10万件,现从各自生产的产品中分别随机抽取20件,进行品质鉴定,鉴定成绩的茎叶图如图所示:
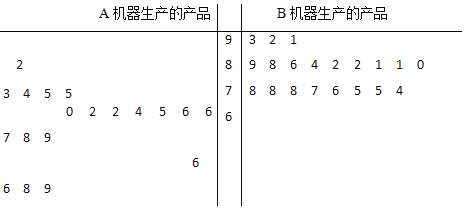
该产品的质量评价标准规定:鉴定成绩达到![]() 的产品,质量等级为优秀;鉴定成绩达到
的产品,质量等级为优秀;鉴定成绩达到![]() 的产品,质量等级为良好;鉴定成绩达到
的产品,质量等级为良好;鉴定成绩达到![]() 的产品,质量等级为合格
的产品,质量等级为合格![]() 将这组数据的频率视为整批产品的概率.
将这组数据的频率视为整批产品的概率.
![]() Ⅰ
Ⅰ![]() 从等级为优秀的样本中随机抽取两件,记X为来自B机器生产的产品数量,写出X的分布列,并求X的数学期望;
从等级为优秀的样本中随机抽取两件,记X为来自B机器生产的产品数量,写出X的分布列,并求X的数学期望;
![]() Ⅱ
Ⅱ![]() 完成下列
完成下列![]() 列联表,以产品等级是否达到良好以上
列联表,以产品等级是否达到良好以上![]() 含良好
含良好![]() 为判断依据,判断能不能在误差不超过
为判断依据,判断能不能在误差不超过![]() 的情况下,认为B机器生产的产品比A机器生产的产品好;
的情况下,认为B机器生产的产品比A机器生产的产品好;
A生产的产品 | B生产的产品 | 合计 | |
良好以上 | |||
合格 | |||
合计 |
![]() 已知优秀等级产品的利润为12元
已知优秀等级产品的利润为12元![]() 件,良好等级产品的利润为10元
件,良好等级产品的利润为10元![]() 件,合格等级产品的利润为5元
件,合格等级产品的利润为5元![]() 件,A机器每生产10万件的成本为20万元,B机器每生产10万件的成本为30万元;该工厂决定:按样本数据测算,两种机器分别生产10万件产品,若收益之差达到5万元以上,则淘汰收益低的机器,若收益之差不超过5万元,则仍然保留原来的两台机器
件,A机器每生产10万件的成本为20万元,B机器每生产10万件的成本为30万元;该工厂决定:按样本数据测算,两种机器分别生产10万件产品,若收益之差达到5万元以上,则淘汰收益低的机器,若收益之差不超过5万元,则仍然保留原来的两台机器![]() 你认为该工厂会仍然保留原来的两台机器吗?
你认为该工厂会仍然保留原来的两台机器吗?
附:![]() 独立性检验计算公式:
独立性检验计算公式:![]() .
.
![]() 临界值表:
临界值表:
|
|
|
|
|
|
k |
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( ) 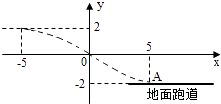
A.y= ![]() ﹣
﹣ ![]() x
x
B.y= ![]() x3﹣
x3﹣ ![]() x
x
C.y= ![]() x3﹣x
x3﹣x
D.y=﹣ ![]() x3+
x3+ ![]() x
x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com