
【题目】某工厂为了提高生产效率,对生产设备进行了技术改造,为了对比技术改造后的效果,采集了技术改造前后各20次连续正常运行的时间长度(单位:天)数据,整理如下:
改造前:19,31,22,26,34,15,22,25,40,35,18,16,28,23,34,15,26,20,24,21
改造后:32,29,41,18,26,33,42,34,37,39,33,22,42,35,43,27,41,37,38,36
(1)完成下面的列联表,并判断能否有99%的把握认为技术改造前后的连续正常运行时间有差异?
超过30 | 不超过30 | |
改造前 | ||
改造后 |
(2)工厂的生产设备的运行需要进行维护,工厂对生产设备的生产维护费用包括正常维护费,保障维护费两种.对生产设备设定维护周期为T天(即从开工运行到第kT天,k∈N*)进行维护.生产设备在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产设备能连续运行,则只产生一次正常维护费,而不会产生保障维护费;若生产设备不能连续运行,则除产生一次正常维护费外,还产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产设备一个生产周期(以120天计)内的维护方案:T=30,k=1,2,3,4.以生产设备在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及均值.
附: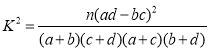
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【答案】(1)见解析,有99%的把握认为技术改造前后的连续正常运行时间有差异.(2)见解析;均值为2.275万元.
【解析】
(1)根据已知改造前后数据完成![]() 列联表,计算
列联表,计算![]() ,查表与临界值比较大小即可确定;
,查表与临界值比较大小即可确定;
(2)依题意可知,一个维护周期内,生产线需保障维护的概率为![]() ,一个生产周期内需保障维护的次数服从二项分布.计算出一个生产周期内的正常维护费和保障维护费即可得出一个生产周期内的生产维护费,根据二项分布概率公式可求出分布列及期望.
,一个生产周期内需保障维护的次数服从二项分布.计算出一个生产周期内的正常维护费和保障维护费即可得出一个生产周期内的生产维护费,根据二项分布概率公式可求出分布列及期望.
解:(1)列联表为:
超过30 | 不超过30 | |
改造前 | 5 | 15 |
改造后 | 15 | 5 |
![]()
![]() 有99%的把握认为技术改造前后的连续正常运行时间有差异.
有99%的把握认为技术改造前后的连续正常运行时间有差异.
(2)由题知,生产周期内有4个维护周期,一个维护周期为30天,一个维护周期内,生产线需保障维护的概率为![]() .
.
设一个生产周期内需保障维护的次数为![]() ,则
,则![]() ;一个生产周期内的正常维护费为
;一个生产周期内的正常维护费为![]() 万元,保障维护费为
万元,保障维护费为![]() 万元.
万元.
![]() 一个生产周期内需保障维护
一个生产周期内需保障维护![]() 次时的生产维护费为
次时的生产维护费为![]() 万元.
万元.
设一个生产周期内的生产维护费为X,则X的所有可能取值为2,2.2,2.6,3.2,4.
![]()
![]()
![]()
![]()
![]()
所以,![]() 的分布列为
的分布列为
| 2 | 2.2 | 2.6 | 3.2 | 4 |
|
|
|
|
|
|
![]()
![]()
![]() 一个生产周期内生产维护费的均值为2.275万元.
一个生产周期内生产维护费的均值为2.275万元.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
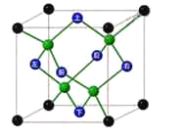
【题目】金刚石是碳原子的一种结构晶体,属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元),即碳原子处在立方体的![]() 个顶点,
个顶点,![]() 个面的中心,此外在立方体的对角线的
个面的中心,此外在立方体的对角线的![]() 处也有
处也有![]() 个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有
个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有![]() 个按照正四面体分布的碳原子.设金刚石晶胞的棱长为
个按照正四面体分布的碳原子.设金刚石晶胞的棱长为![]() ,则正四面体
,则正四面体![]() 的棱长为__________;正四面体
的棱长为__________;正四面体![]() 的外接球的体积是__________.
的外接球的体积是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项数学竞赛考试共四道题,考察内容分别为代数、几何、数论、组合,已知前两题每题满分40分,后两题每题满分60分,题目难度随题号依次递增,已知学生甲答题时,若该题会做则必得满分,若该题不会做则不作答得0分,通过对学生甲以往测试情况的统计,得到他在同类模拟考试中各题的得分率,如表所示:

假设学生甲每次考试各题的得分相互独立.
(1)若此项竞赛考试四道题的顺序依次为代数、几何、数论、组合,试预测学生甲考试得160分的概率;
(2)学生甲研究该项竞赛近五年的试题发现第1题都是代数题,于是他在赛前针对代数版块进行了强化训练,并取得了很大进步,现在,只要代数题是在试卷第1、2题的位置,他就一定能答对,若今年该项数学竞赛考试四道题的顺序依次为代数、数论、组合、几何,试求学生甲此次考试得分X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数g(x)=sinωx(ω>0)向左平移![]() 个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
A.f(x)的图象关于直线![]() 对称
对称
B.f(x)在(0,2π)上有且只有3个极大值点,f(x)在(0,2π)上有且只有2个极小值点
C.f(x)在![]() 上单调递增
上单调递增
D.ω的取值范围是[![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点![]() 是由
是由![]() 绕直线
绕直线![]() 旋转得到,连结
旋转得到,连结![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“![]() ”表示一个阳爻,“
”表示一个阳爻,“![]() ”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )
”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 图象在
图象在![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() 存在极大值和极小值,且极大值小于极小值,求
存在极大值和极小值,且极大值小于极小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com