
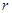 米,高为
米,高为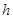 米,体积为
米,体积为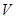 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为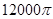 元(
元(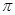 为圆周率).
为圆周率).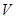 表示成
表示成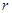 的函数
的函数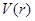 ,并求该函数的定义域;
,并求该函数的定义域;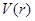 的单调性,并确定
的单调性,并确定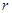 和
和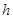 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大. 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 是边长为
是边长为 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
. 最大,试问
最大,试问 应取何值?
应取何值? 最大,试问
最大,试问 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 万件,需另投入的成本为
万件,需另投入的成本为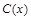 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完. (万元)关于年产量
(万元)关于年产量 (万件)的函数关系式;
(万件)的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.49 h | B.56 h | C.64 h | D.72 h |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.上午10:00 | B.中午12:00 |
| C.下午4:00 | D.下午6:00 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.f(5)=1 |
B.方程f(x)= 有且仅有一个解 有且仅有一个解 |
| C.函数f(x)是周期函数 |
| D.函数f(x)是减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com