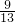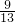A
分析:由α的范围,及cosα的值,利用同角三角函数间的基本关系求出sinα的值,再利用同角三角函数间的基本关系求出tanα的值,然后将所求式子中的角β变为α-(α-β),利用两角和与差的正切函数公式化简后,将tanα及tan(α-β)的值代入,即可求出值.
解答:∵α∈(

,2π),cosα=

,
∴sinα=-
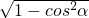
=-

,
∴tanα=

=-

,又tan(α-β)=-

,
则tanβ=tan[α-(α-β)]
=
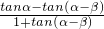
=
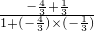
=-
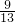
.
故选A
点评:此题考查了同角三角函数间的基本关系,以及两角和与差的正切函数公式,熟练掌握公式及基本关系是解本题的关键,同时注意角度的范围.

 ,
,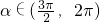 ,
,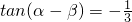 则tanβ的值是
则tanβ的值是