练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数的定义域为，对于定义域内的任意实数，有成立，且时，.

    （1）当时，求函数的最大值；

    （2）当时，求函数的最大值；

    （3）已知（实数），求实数的最小值.

    【答案】（1）4 （2）5.6 （3）

    【解析】

    （1）根据定义可知,依次代入各段定义域,即可求得当时函数的解析式,即可求得最大值.

    （2）先判断出,并求得当时的解析式,根据函数单调性,代入即可求解.

    （3）求得当时的解析式,根据,代入解析式,并结合,即可求得的最小值及的最小值.

    （1）因为函数的定义域为,对于定义域内的任意实数,有成立,

    则

    当时,.值域为

    当时,,值域为

    当时,,值域为

    综上可知,当时,函数的最大值为.

    （2）由（1）可知

    当时,

    且函数为单调递增函数

    所以最大值为

    故最大值为

    （3）由（1）可知,当时,

    而,所以

    则设,则

    所以,

    ,则

    所以的最小值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，已知平面，且四边形为直角梯形，，，.

    （1）证明：；

    （2）求平面与平面所成锐二面角的余弦值；

    （3）点是线段上的动点，当直线与所成的角最小时，求线段的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，直线分别交轴、轴的正半轴于、两点，为坐标原点.

    （1）若直线方程为（），且，求的值；

    （2）若直线经过点，设的斜率为，为线段的中点，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在锐角△ABC中，分别为A、B、C所对的边，且

    （1）确定角C的大小；

    （2）若c＝，求△ABC周长的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是定义域为的奇函数，且当时， ，设 “”.

    （1）若为真，求实数的取值范围；

    （2）设集合与集合的交集为，若为假， 为真，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校举行汉字听写比赛，为了了解本次比赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数，满分100分)进行统计，请根据频率分布表中所提供的数据，解答下列问题：

    （1）求的值；

    （2）若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛，并从中选出2人做种子选手，求2人中至少有1人是第4组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知不共线向量，满足||＝3，||＝2，（23）（2）＝20.

    （1）求；

    （2）是否存在实数λ，使λ与2共线？

    （3）若（k2）⊥（），求实数k的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

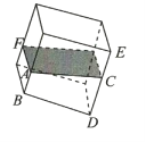
    【题目】在一个长方体的容器中，里面装有少量的水，现在将容器绕着其底部的一条棱倾斜．

    （1）在倾斜的过程中，水面的形状不断变化，可能是矩形，也可能变成不是矩形的平行四边形，对吗？

    （2）在倾斜的过程中，水的形状也不断变化，可以是棱柱，也可能变为棱台或棱锥，对吗？

    （3）如果倾斜时，不是绕着底部的一条棱，而是绕着其底面的一个顶点，上面的第（1）问和第（2）问对不对？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知（为自然对数的底数）．

    （1）若在处的切线过点，求实数的值；

    （2）当时，恒成立，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案