
【题目】“节能减排,绿色生态”为当今世界各国所倡导,某公司在科研部门的鼎力支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该公 司每月的处理量![]() (吨)至少为50吨,至多为220吨.月处理成本
(吨)至少为50吨,至多为220吨.月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系式近似表示为:
(吨)之间的函数关系式近似表示为:![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为120元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为120元.
(1)该公司每月处理量为多少吨时,才能使每吨的平均处理成本![]() 最低?
最低?
(2)每月处理量为多少吨时,月获利最大?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B.对于命题![]() :
:![]() ,使得
,使得![]() ,则
,则![]() :
:![]() 均有
均有![]()
C.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
D.命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 中有:①若
中有:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() —定为等腰三角形;③若
—定为等腰三角形;③若![]() ,则
,则![]() —定为直角三角形;④若
—定为直角三角形;④若![]() ,且该三角形有两解,则
,且该三角形有两解,则![]() 的范围是
的范围是![]() .以上结论中正确的个数有( )
.以上结论中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
![]()
![]() ,若
,若![]() ,且
,且![]() 的图象相邻的对称轴间的距离不小于
的图象相邻的对称轴间的距离不小于![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)若当![]() 取最大值时,
取最大值时, ![]() ,且在
,且在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,其面积
的对边,其面积![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点 .
的中点 .
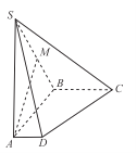
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一座小岛距离海岸线上最近的点P的距离是3 km,从点P沿海岸正东12 km处有一个渔村.
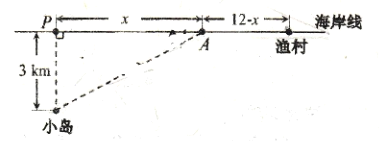
(1)假设一个人驾驶的小船的平均速度为![]() ,步行的速度是
,步行的速度是![]() .y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
.y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
(2)在(1)的条件下,是否有一个停船的位置使得从小岛到渔村花费的时间最少?说明理由.(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A.一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
B.平行于同一个平面的两个不同平面平行
C.若直线l与平面![]() 平行,则过平面
平行,则过平面![]() 内一点且与直线l平行的直线在平面
内一点且与直线l平行的直线在平面![]() 内
内
D.若直线l不平行于平面![]() ,则在平面
,则在平面![]() 内不存在与l平行的直线
内不存在与l平行的直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com