
【题目】已知函数f(x)=axlnx﹣x+l (a∈R),且f(x)≥0.
(I)求a;
( II)求证:当,n∈N*时, ![]()
【答案】(1)1(2)见解析
【解析】试题分析:(Ⅰ)通过讨论![]() 的范围,求出函数的单调区间,求出函数的最小值,问题转化为
的范围,求出函数的单调区间,求出函数的最小值,问题转化为![]() ,令
,令![]() ,求出
,求出![]() 的最小值,求出
的最小值,求出![]() 的值即可;(Ⅱ)由
的值即可;(Ⅱ)由![]() 恒成立.令
恒成立.令![]() ,根据取值累加即可.
,根据取值累加即可.
试题解析:(Ⅰ)f(x)的定义域为(0,+∞).
若a<0,f(2)=2aln2﹣1<0,与已知矛盾.…
若a=0,则f(x)=﹣x+1,显然不满足在(0,+∞)上f(x)≥0恒成立.…
若a>0,对f(x)求导可得f'(x)=alnx+a﹣1.
由f'(x)>0解得![]() ,由f'(x)<0解得0<
,由f'(x)<0解得0<![]() ,
,
∴f(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴f(x)min=![]() =1﹣a
=1﹣a![]() . …
. …
∴要使f(x)≥0恒成立,则须使1﹣a![]() ≥0成立,即
≥0成立,即![]() ≤
≤![]() 恒成立.
恒成立.
两边取对数得,![]() ≤ln
≤ln![]() ,整理得lna+
,整理得lna+![]() ﹣1≤0,即须此式成立.
﹣1≤0,即须此式成立.
令g(a)=lna+![]() ﹣1,则
﹣1,则![]() ,
,
显然当0<a<1时,g'(a)<0,当a>1时,g'(a)>0,
于是函数g(a)在(0,1)上单调递减,在(1,+∞)单调递增,
∴g(a)min=g(1)=0,
即当且仅当a=1时,f(x)min=f(1)=0,f(x)≥0恒成立,
∴a=1满足条件.
综上,a=1.…
(Ⅱ)由(Ⅰ)知x>1时,xlnx﹣x+1>0,即lnx>![]() 恒成立.
恒成立.
令![]() (n∈N*),即
(n∈N*),即![]() >
>![]() ,
,
即![]() ,…
,…
同理,![]() ,
,
![]() ,…,
,…,
![]() ,
,
![]() ,…
,…
将上式左右相加得:
![]()
=![]() =ln4.=2ln2…
=ln4.=2ln2…


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的矩形![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 边上异于
边上异于![]() ,
, ![]() 两点的动点,且
两点的动点,且![]() ,
, ![]() 为线段
为线段![]() 的中点,现沿
的中点,现沿![]() 将四边形
将四边形![]() 折起,使得
折起,使得![]() 与
与![]() 的夹角为
的夹角为![]() ,连接
,连接![]() ,
, ![]() .
.

(1)探究:在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,说明点
,若存在,说明点![]() 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
(2)求三棱锥![]() 的体积的最大值,并计算此时
的体积的最大值,并计算此时![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=![]() ,其前n项和为Sn,且Sn=an+1-
,其前n项和为Sn,且Sn=an+1-![]() (n∈N*).
(n∈N*).
(1)求an,Sn;
(2)设bn=log2(2Sn+1)-2,数列{cn}满足cn·bn+3·bn+4=1+(n+1)(n+2)·2bn,数列{cn}的前n项和为Tn,求使4Tn>2n+1-![]() 成立的最小正整数n的值.
成立的最小正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与半径
的垂直平分线与半径![]() 交于
交于![]() 点,当点
点,当点![]() 在圆
在圆![]() 上运动时,
上运动时,
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 作直线
作直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,求
为坐标原点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin 2x-
sin 2x-![]() cos2x.
cos2x.
(1)求f(x)的周期和最小值;
(2)将函数f(x)的图像上每一点的横坐标伸长到原来的两倍(纵坐标不变),再把所得图像上的所有点向上平移![]() 个单位,得到函数g(x)的图像,当
个单位,得到函数g(x)的图像,当![]() 时,求g(x)的值域.
时,求g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点, ![]() ,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
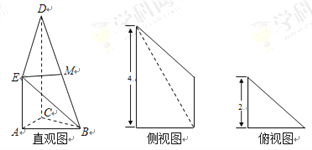
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系和直角坐标系中,极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合,曲线
轴的非负半轴重合,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)判断曲线![]() 与曲线
与曲线![]() 的位置关系,若两曲线相交,求出两交点间的距离.
的位置关系,若两曲线相交,求出两交点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com