Question

（09年西城区抽样文）（14分）

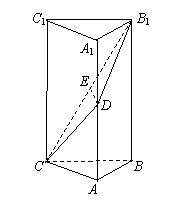
    如图，在直三棱柱中，，D、E分别是AA₁、B₁C的中点.

(Ⅰ) 求证：平面；

 (Ⅱ) 求异面直线与所成角的大小；

(Ⅲ) 求二面角C-B₁D-B的大小.

Answer 1

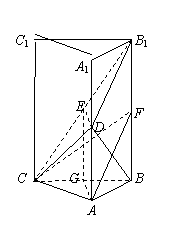
解析：方法一：（Ⅰ）证明：如图，设G为BC的中点，连接EG，AG，

在中，，

      ，且，

      又，且，       

      ，

      四边形为平行四边形，

      ，                                     ------------------------2分

      又平面ABC，平面ABC，

      平面.                                --------------------------4分

（Ⅱ）解：如图，设F为BB₁的中点，连接AF，CF，

      直三棱柱，且D是AA₁的中点，

      ，

      为异面直线与所成的角或其补角.           -------------------7分

     在Rt中，，AB=1，BF=1，

     ，同理，

     在中，，

     在中，，

.

     异面直线与所成的角为.                  ----------------------9分

（Ⅲ）解：直三棱柱，，

      又，

平面.                                ----------------------10分

如图，连接BD，

在中，，

，即，

是CD在平面内的射影，

，

为二面角C-B₁D-B的平面角.                   --------------------12分

在中, , BC=1, ，

,

二面角C-B₁D-B的大小为.                  --------------------14分

  方法二：（Ⅰ）同方法一.                                 ----------------------4分

（Ⅱ）如图，以B为原点，BC、BA、BB₁分别为x、y、z轴，建立空间直角坐标系O-xyz，

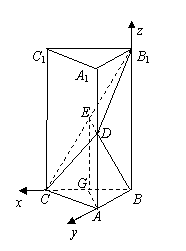
 则，

        ,                    ----------------------6分

，

异面直线与所成的角为.               ----------------------9分

（Ⅲ）解：直三棱柱，，

      又，

平面.         ---------------------------10分                         

如图，连接BD，

在中，，

，即，

是CD在平面内的射影，

，

      为二面角C-B₁D-B的平面角.                -----------------------12分

，

，

         二面角C-B₁D-B的大小为.             ------------------------14分