
分析 (1)运用单调性的定义,设值、作差、变形和定符号、下结论等;
(2)运用定义法,若f(x)为奇函数,可得f(-x)+f(x)=0,化简整理,解方程即可得到a的值.
解答 解:(1)证明:设m<n,
则f(m)-f(n)=a-$\frac{2}{{2}^{m}+1}$-(a-$\frac{2}{{2}^{n}+1}$)
=$\frac{2({2}^{m}-{2}^{n})}{({2}^{m}+1)({2}^{n}+1)}$,
由m<n,可得2m<2n,则(2m+1)(2n+1)>0,2m-2n<0.
即有f(m)-f(n)<0,即f(m)<f(n),
则f(x)在R上为增函数;
(2)存在实数a=1,使函数f(x)为奇函数.
若f(x)为奇函数,可得f(-x)+f(x)=0,
即有a-$\frac{2}{{2}^{-x}+1}$+a-$\frac{2}{{2}^{x}+1}$=2a-($\frac{2•{2}^{x}}{1+{2}^{x}}$+$\frac{2}{{2}^{x}+1}$)
=2a-2=0,
解得a=1.
点评 本题考查函数的单调性的判断,注意运用定义法,考查存在性问题的解法,注意运用假设法,以及奇函数的定义,考查运算能力,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:填空题
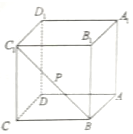 如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1] | B. | (-∞,-2) | C. | [-$\frac{5}{2}$,4] | D. | [-2,$\frac{7}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
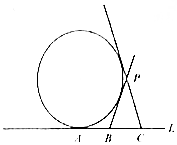 如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)
如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com