
| A. | $\frac{{5\sqrt{42}}}{2}$ | B. | $5\sqrt{42}$ | C. | $5\sqrt{3}$ | D. | $5\sqrt{14}$ |
分析 求出$\overrightarrow{AB}$=(3,4,-8),$\overrightarrow{AC}$=(5,1,-7),△ABC的面积S=$\frac{1}{2}×|\overrightarrow{AB}|×|\overrightarrow{AC}|×sin<\overrightarrow{AB},\overrightarrow{AC}>$,由此能求出结果.
解答 解:∵A(1,-2,11),B(4,2,3),C(6,-1,4),
∴$\overrightarrow{AB}$=(3,4,-8),$\overrightarrow{AC}$=(5,1,-7),
|$\overrightarrow{AB}$|=$\sqrt{9+16+64}$=$\sqrt{89}$,
|$\overrightarrow{AC}$|=$\sqrt{25+1+49}$=5$\sqrt{3}$,
cos<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}|•|\overrightarrow{AC}|}$=$\frac{15+4+56}{\sqrt{89}•5\sqrt{3}}$=$\frac{5\sqrt{3}}{\sqrt{89}}$,
sin<$\overrightarrow{AB},\overrightarrow{AC}$>=$\sqrt{1-(\frac{5\sqrt{3}}{\sqrt{89}})^{2}}$=$\frac{\sqrt{14}}{\sqrt{89}}$,
∴△ABC的面积S=$\frac{1}{2}×|\overrightarrow{AB}|×|\overrightarrow{AC}|×sin<\overrightarrow{AB},\overrightarrow{AC}>$=$\frac{1}{2}×\sqrt{89}×5\sqrt{3}×\frac{\sqrt{14}}{\sqrt{89}}$=$\frac{5\sqrt{42}}{2}$.
故选:A.
点评 本题考查三角形面积的求法,是基础题,解题时要认真审题,注意空间向量坐标运算法则的合理运用.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
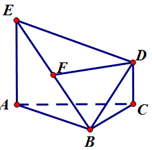 如图,△ABC为等边三角形,EA⊥平面ABC,EA∥DC,EA=2DC,F为EB的中点.
如图,△ABC为等边三角形,EA⊥平面ABC,EA∥DC,EA=2DC,F为EB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com