练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设f（x）=log2（2+|x|）﹣ ，则使得f（x﹣1）＞f（2x）成立的x取值范围是 ．

    【答案】（﹣1, ）
    【解析】解：函数f（x）=log2（2+|x|）﹣ ，是偶函数，

    当x≥0时，y=log2（2+x），y=﹣ 都是增函数，所以f（x）=log2（2+x）﹣ ，x≥0是增函数，

    f（x﹣1）＞f（2x），可得|x﹣1|＞|2x|，可得3x2+2x﹣1＜0，解得x∈（﹣1， ）．

    所以答案是：（﹣1， ）．

    【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 为偶函数．
    （1）求实数t值；
    （2）记集合E={y|y=f（x），x∈{1，2，3}}，λ=lg22+lg2lg5+lg5﹣1，判断λ与E的关系；
    （3）当x∈[a，b]（a＞0，b＞0）时，若函数f（x）的值域为[2﹣ ，2﹣ ]，求实数a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一辆汽车在某段路程中的行驶速率与时间的关系如图所示．
    （1）求图中阴影部分的面积，并说明所求面积的实际含义；
    （2）假设这辆汽车在行驶该段路程前里程表的读数是8018km，试求汽车在行驶这段路程时里程表读数s（km）与时间t （h）的函数解析式，并作出相应的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】要得到函数y=log2（2x+1）的图象，只需将y=1+log2x的图象（ ）
    A.向左移动 个单位
    B.向右移动 个单位
    C.向左移动1个单位
    D.向右移动1个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】北京市为了缓解交通压力，计划在某路段实施“交通限行”，为调查公众对该路段“交通限行”的态度，某机构从经过该路段的人员中随机抽查了80人进行调查，将调查情况进行整理，制成表：

    年龄（岁）

    [15，30）

    [30，45）

    [45，60）

    [60，75）

    人数

    24

    26

    16

    14

    赞成人数

    12

    14

    x

    3


    （1）若经过该路段的人员对“交通限行”的赞成率为0.40，求x的值；
    （2）在（1）的条件下，若从年龄在[45，60），[60，75）内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访，求选中的2人中至少有1人来自[60，75）内的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}中，a1=2，a2=6，且数列{an﹣1﹣an}{n∈N*}是公差为2的等差数列．
    （1）求{an}的通项公式；
    （2）记数列{ }的前n项和为Sn ， 求满足不等式Sn＞ 的n的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现代城市大多是棋盘式布局（如上海道路几乎都是东西和南北走向）．在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离（位移），而是实际路程（如图）．在直角坐标平面内，我们定义A（x1 ， y1）、B（x2 ， y2）两点间的“直角距离”为：D（AB）=|x1﹣x2|+|y1﹣y2|．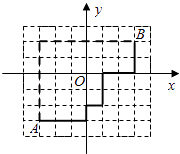

    （1）在平面直角坐标系中，写出所有满足到原点的“直角距离”
    为2的“格点”的坐标；（格点指横、纵坐标均为整数的点）
    （2）定义：“圆”是所有到定点“直角距离”为定值的点组成的图形，点A（1，3），B（1，1），C（3，3），求经过这三个点确定的一个“圆”的方程，并画出大致图象；
    （3）设P（x，y），集合B表示的是所有满足D（PO）≤1的点P所组成的集合，
    点集A={（x，y）|﹣1≤x≤1，﹣1≤y≤1}，
    求集合Q={（x，y）|x=x1+x2 ， y=y1+y2 ， （x1 ， y1）∈A，（x2 ， y2）∈B}所表示的区域的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知锐角△ABC的三内角A，B，C所对的边分别是a，b，c，且2csinB= b．
    （1）求角C的大小；
    （2）若边c=1，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 是奇函数，f（x）=lg（10x+1）+bx是偶函数．
    （1）求a+b的值．
    （2）若对任意的t∈[0，+∞），不等式g（t2﹣2t）+g（2t2﹣k）＞0恒成立，求实数k的取值范围．
    （3）设 ，若存在x∈（﹣∞，1]，使不等式g（x）＞h[lg（10a+9）]成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案