练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，两铁路线垂直相交于站A，若已知AB＝100公里，甲火车从A站出发，沿AC方向以50公里/小时的速度行驶，同时乙火车以V公里/小时的速度从B站沿BA方向行驶，行驶至A站时即停止(甲车仍继续行驶)．

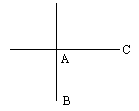
    (1)求甲、乙两车的最近距离(两车的车长忽略不计)；

    (2)若甲、乙两车开始行驶到甲、乙两车相距最近所用时间为t0小时，问V为何值时，t0最大．

    答案：
    解析：

    		 　　(1)设乙车行驶t小时到D，甲车行驶t小时到E， 　　若0≤tV≤100

    　　(1)设乙车行驶t小时到D，甲车行驶t小时到E，　　若0≤tV≤100．

    　　则DE2＝AE2＋AD2＝(100－tV)2＋(50t)2＝(2500＋V2)t2－200Vt＋10000

    　　当t＝时，DE2取最小值，DE也取最小值，其最小值为

    　　　　若tV＞100时，乙车停止，甲车继续前行，DE越来越大，无最大值．

    　　由、知，甲、乙两车的最近距离为公里

    　　(2)t0＝＝≤＝1，当且仅当V＝

    　　即V＝50公里／小时时，t0最大．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    如图：A、B是两个定点，且|AB|＝2，动点M到A点的距离是4，线段MB的垂直平分线l交MA于点P，直线k垂直于直线AB，且B点到直线k的距离为3．

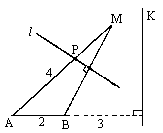
    (Ⅰ)建立适当的坐标系，求动点P的轨迹方程；

    (Ⅱ)求证：点P到点B的距离与点P到直线k的距离之比为定值；

    (Ⅲ)(理)若点P到A、B两点的距离之积为m，当m取最大值时，求P点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    如图所示，设C(a，b)是定点(ab≠0)，过C作两条互相垂直的直线l1和l2，且l1，l2分别交x，y轴于A，B，求：

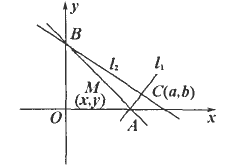
    (1)线段AB中点M的轨迹方程；

    (2)|MC|的最小值．

    查看答案和解析>>

    科目：高中数学 来源：龙门中学、新丰一中、连平中学三校联考试题、高三数学(理) 题型：044

    解答题

    如图，已知E、F为平面上的两个定点，(G为动点，P是HP和GF的交点)

    (1)

    建立适当的平面直角坐标系求出点的轨迹方程；

    (2)

    若点的轨迹上存在两个不同的点、，且线段的中垂线与

    (或的延长线)相交于一点，则＜(为的中点)．

    查看答案和解析>>

    科目：高中数学 来源：广东省珠海市斗门一中2006－2007高三数学理科第一次月考试卷、新课标　人教版 人教版　新课标 题型：044

    解答题

    如图，在四棱锥P—ABCD中，PA、AB、AD两两互相垂直，AB∥CD，且CD＝2AB，E是PC的中点．

    (1)

    求证：BE∥平面PAD；

    (2)

    当平面PCD与平面ABCD成多大角时，BE⊥平面PCD？

    查看答案和解析>>

    同步练习册答案