
下列各组对象:
①接近于0的数的全体;
②比较小的正整数全体;
③平面上到点O的距离等于1的点的全体;
④正三角形的全体;
⑤![]() 的近似值的全体.
的近似值的全体.
其中能构成集合的组数是
A.2
B.3
C.4
D.5
“接近于0的数”、“比较小的正整数”标准不明确,即元素不确定,所以①、②不是集合.同样,“![]() 的近似值”也不明确精确到什么程度,因此很难判定一个数,比如2是不是它的近似值,所以⑤也不是一个集合.③、④能构成集合.∴选A.
的近似值”也不明确精确到什么程度,因此很难判定一个数,比如2是不是它的近似值,所以⑤也不是一个集合.③、④能构成集合.∴选A.
一些元素构成的集合必须具有以下两个特点:一是整体性,二是确定性.其中“整体”一词,说明集合是指某些对象的整体而不是指其中的个别对象,这就是集合的整体性.“一些元素”一词,说明集合是由属于它的元素所完全确定的,一个对象要么是集合的元素,要么不是集合的元素,二者必居其一,这是集合的确定性.
由此可见,只要元素是确定的,看做一个整体,便形成一个集合.否则,不然.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:013
下列各组对象
(1)接近于0的数的全体;
(2)比较小的正整数全体;
(3)平面上到点O的距离等于1的点的全体;
(4)正三角形的全体;
(5)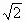 的近似值的全体.
的近似值的全体.
其中能构成集合的组数是
[ ]
查看答案和解析>>
科目:高中数学 来源:学习高手必修一数学苏教版 苏教版 题型:044
指出下列各组对象是否能组成集合,若能组成集合则指出集合是有限集,还是无限集,还是空集.
(1)平方等于1的数;
(2)所有的矩形;
(3)著名的数学家;
(4)非常接近于10的数;
(5)平面直角坐标系中,第四象限的点;
(6)被5除余数是2的正数;
(7)平方后等于-1的实数;
(8)15的正约数.
判断一个集合是有限集、空集还是无限集的关键是看集合中元素的个数.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
下列各组对象
(1)接近于0的数的全体;
(2)比较小的正整数全体;
(3)平面上到点O的距离等于1的点的全体;
(4)正三角形的全体;
(5)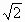 的近似值的全体.
的近似值的全体.
其中能构成集合的组数是
[ ]
查看答案和解析>>
科目:高中数学 来源: 题型:
①一切很大的数;
②接近于0的数的全体;
③聪明人;
④正三角形的全体;
⑤方程x2=-2的实数根;
⑥平面上到定点O的距离等于1的点的全体.
其中能构成集合的组数是( )
A.2 B.3
C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com