考点:利用导数研究函数的单调性
专题:导数的综合应用
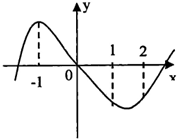
分析:由图象可知:经过原点,可得f(0)=0=d,即f(x)=ax
3+bx
2+cx..由图象可得:函数f(x)在[-1,1]上单调递减,函数f(x)在x=-1处取得极大值.可得f′(x)≤0在[-1,1]上恒成立,且f′(-1)=0.利用且f′(1)<0,f′(2)>0即可得到b<0,3a+2b>0,设k=
,则k=
,求k的最值,进而得出结论.
解答:解:由图象可知:经过原点,∴f(0)=0=d,
∴f(x)=ax
3+bx
2+cx.
由图象可得:函数f(x)在[-1,1]上单调递减,函数f(x)在x=-1处取得极大值.
∴f′(x)=3ax
2+2bx+c≤0在[-1,1]上恒成立,且f′(-1)=0.
得到3a-2b+c=0,即c=2b-3a,
∵f′(1)=3a+2b+c<0,
∴4b<0,即b<0,
∵f′(2)=12a+4b+c>0,
∴3a+2b>0,
设k=
,则k=
,
建立如图所示的坐标系,则点A(-1,-2),
则k=
式中变量a、b满足下列条件
,
作出可行域如图:
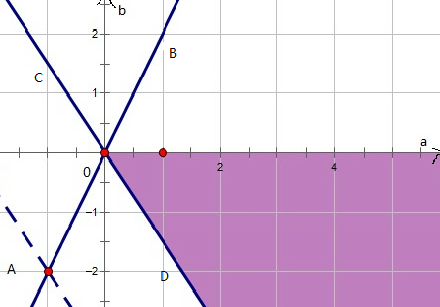
∴k的最大值就是k
AB=
,k的最小值就是k
CD,而k
CD就是直线3a+2b=0的斜率,k
CD=-
,
∴
-<k<.
∴故选A.
点评:本题综合考查了利用导数研究函数的单调性极值、数形结合等基础知识与基本方法.




 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案