
| A. | $\frac{a(2a+l)}{{2\sqrt{{a^2}+{b^2}}}}$ | B. | $\frac{a+l}{{2\sqrt{{a^2}+{b^2}}}}$ | C. | $\frac{a(l-2a)}{{2\sqrt{{a^2}+{b^2}}}}$ | D. | $\frac{al}{{2\sqrt{{a^2}+{b^2}}}}$ |
分析 用A、B 两点的坐标表示出|FA|和|FB|,解出A、B 两点的坐标,利用|FA|+|FB|≥|AB|,求得m的最小值.
解答 解:设AB中点M的横坐标为m,右焦点为F,离心率为e,AB的中点横坐标为m,
则m=$\frac{1}{2}$(xA+xB),
|FA|=e(xA-$\frac{{a}^{2}}{c}$),|FB|=e(xB-$\frac{{a}^{2}}{c}$),
∴m=$\frac{1}{2}$•$\frac{1}{e}$(|FA|+|FB|)+$\frac{{a}^{2}}{c}$≥$\frac{1}{2e}$|AB|+$\frac{{a}^{2}}{c}$=$\frac{1}{2e}$+$\frac{{a}^{2}}{c}$=$\frac{la}{2c}$+$\frac{{a}^{2}}{c}$
=$\frac{a(2a+l)}{2\sqrt{{a}^{2}+{b}^{2}}}$,
当且仅当F、A、B共线时,m取得最小值.
故选:A.
点评 本题考查双曲线的定义和双曲线的标准方程、以及双曲线的简单性质的应用,注意运用双曲线的第二定义,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | -$\frac{2\sqrt{3}}{9}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 16 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{4}{3}$,4] | B. | [$\frac{4}{3}$,4) | C. | [2,4] | D. | (2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
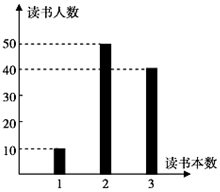 某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com